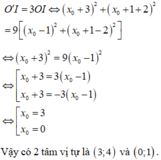Cho đường tròn (0;R) và một diem A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. CMR BAC=60°khi và chỉ khi OA=2R

Những câu hỏi liên quan
Cho hai đường tròn (0) (0) cắt nhau tại hai điểmA và B. các đường thẳng AO,AO cắt đường tròn (0) lần lượt tại các điểm thứ haiC,D và cắt đường tròn(0) tại điểm thứ hai E,F a. Chứng minh B,F,C thẳng hàngb.Chứng minh AB,CD,FE đồng quyc.Chứng minh tứ giác CDEF nội tiếpd.Chứng minh A là tâm đường tròn nội tiếp tam giácBDEe.MN là một tiếp tuyến chung của(0) và (0) (M,N là tiếp diễn) chứng minh AB đi qua chúng điểm của MNf....
Đọc tiếp
Cho hai đường tròn (0) (0') cắt nhau tại hai điểmA và B. các đường thẳng AO,AO cắt đường tròn (0) lần lượt tại các điểm thứ haiC,D và cắt đường tròn(0') tại điểm thứ hai E,F a. Chứng minh B,F,C thẳng hàng
b.Chứng minh AB,CD,FE đồng quy
c.Chứng minh tứ giác CDEF nội tiếp
d.Chứng minh A là tâm đường tròn nội tiếp tam giácBDE
e.MN là một tiếp tuyến chung của(0) và (0') (M,N là tiếp diễn) chứng minh AB đi qua chúng điểm của MN
f.Tìm điều kiện để DE là tiếp tuyến chung của các đường tròn (0) ,(0').
Bài 4. (3,5 điểm) Cho điểm M nằm ngoài đường tròn (0;R) sao cho OM = 2R. Từ M kẻ các tiếp tuyến MA, MB với đường tròn (0) (A, B là các tiếp điểm). Kẻ đường kính AC của đường tròn (0). Gọi H là giao điểm của AB và OM. 1) Chứng minh bốn điểm A, O, B, M cùng thuộc một đường tròn. 2) Tính tỷ số OH/OM. 3) Gọi E là giao điểm của CM và đường tròn (0). Chứng minh HE vuông góc BE.
Cho đường tròn (C):
x
2
+
y
2
– 2y – 3 0. Đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Ox. Phương trình đường tròn (C’) là: A.
x
2
+
y
2
−
2
y
−
3
0
B.
x
2
+
y
2
+...
Đọc tiếp
Cho đường tròn (C): x 2 + y 2 – 2y – 3 = 0. Đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Ox. Phương trình đường tròn (C’) là:
A. x 2 + y 2 − 2 y − 3 = 0
B. x 2 + y 2 + 2 y − 5 = 0
C. x 2 + y 2 + 2 y − 3 = 0
D. x 2 + y 2 − 2 y − 5 = 0
Đáp án C
(C) có tâm I(0;1) bán kính 2
Đox: I(0;1) -> I’( 0;–1)
Phương trình đường tròn (C’): x 2 + y 2 + 2 y − 3 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ
Ox
y
cho đường tròn
C
:
x
2
+
y
2
−
2
x
−
4
y
+
4
0
và đường tròn
C
:
x
2
+
y
2
+
6
x...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Ox y cho đường tròn C : x 2 + y 2 − 2 x − 4 y + 4 = 0 và đường tròn C ' : x 2 + y 2 + 6 x + 4 y + 4 = 0. Tìm tâm vị tự của hai đường tròn?
A. I 0 ; 1 v à J 3 ; 4
B. I − 1 ; − 2 v à J 3 ; 2
C. I 1 ; 2 v à J − 3 ; − 2
D. I 1 ; 0 v à J 4 ; 3
Đáp án A
Đường tròn C có tâm K 1 ; 2 , bán kính R = 1 + 4 − 4 = 1 .
Đường tròn C ' có tâm K ' − 3 ; − 2 , bán kính R ' = 9 + 4 − 4 = 3.
Giả sử V 1 ; k C = C '
khi đó k = R ' R ⇒ k = 3 ⇔ k = ± 3
Với k = 3 ⇒ I K ' → = 3 I K → ⇒ − 3 − x 1 = 3 1 − x 1 − 2 − y 1 = 3 2 − y 1 ⇒ I 3 ; 4
Với k = − 3 ⇒ I K ' → = − 3 I K → ⇒ − 3 − x 1 = − 3 1 − x 1 − 2 − y 1 = − 3 2 − y 1 ⇒ I 0 ; 1
Đúng 0
Bình luận (0)
Cho đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0. Đường thẳng cắt đường tròn theo dây cung có độ dài là
A.4
B.6
C.8
D.10
(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C
Đúng 0
Bình luận (0)
Cho đường tròn (C):
x
2
+
y
2
+
4
x
−
4
y
−
10
0
và đường thẳng ∆: x + y + m 0. Giá trị m để đường thẳng tiếp xúc với đường tròn là: A.
m
±
6
B.
m
±
3
C.
m
±
8
D.Không tồn tại m
Đọc tiếp
Cho đường tròn (C): x 2 + y 2 + 4 x − 4 y − 10 = 0 và đường thẳng ∆: x + y + m = 0. Giá trị m để đường thẳng tiếp xúc với đường tròn là:
A. m = ± 6
B. m = ± 3
C. m = ± 8
D.Không tồn tại m
Đường tròn (C): x 2 + y 2 + 4 x − 4 y − 10 = 0 có tâm I(-2;2) và bán kính R = 3 2 .
Khoảng cách d ( I ; Δ ) = − 2 + 2 + m 1 2 + 1 2 = m 2
Để đường thẳng tiếp xúc đường tròn thì:
d ( I ; Δ ) = R ⇔ m 2 = 3 2 ⇔ m = 6 ⇔ m = ± 6
ĐÁP ÁN A
Đúng 0
Bình luận (0)
Cho đường tròn tâm (0) và điểm S nằm bên ngoài đường tròn . TừS kẻ tiếp tuyến SA với đường tròn (0) (A là tiếp điểm) a,Chứng tỏ tam giác AOS vuông b,Qua A kẻ đường thẳng vuông góc với OS tại I, cắt đường tròn (0) tại B (B khác A) . C/M SB là tiếp tuyến của đường tròn (O) c,Kẻ đường kính AC của đường tròn (O) . Đường thẳng SC cắt đường tròn tại điểm thứ 2 là D . C/m góc SID góc OCD
Đọc tiếp
Cho đường tròn tâm (0) và điểm S nằm bên ngoài đường tròn . TừS kẻ tiếp tuyến SA với đường tròn (0) (A là tiếp điểm) a,Chứng tỏ tam giác AOS vuông b,Qua A kẻ đường thẳng vuông góc với OS tại I, cắt đường tròn (0) tại B (B khác A) . C/M SB là tiếp tuyến của đường tròn (O) c,Kẻ đường kính AC của đường tròn (O) . Đường thẳng SC cắt đường tròn tại điểm thứ 2 là D . C/m góc SID = góc OCD
a: Xét (O) có
SA là tiếp tuyến
nên SA vuông góc với OA
hay ΔOAS vuông tại A
b: Xét ΔOAS và ΔOBS có
OA=OB
\(\widehat{SOA}=\widehat{SOB}\)
OS chung
Do đó: ΔOAS=ΔOBS
Suy ra: \(\widehat{OAS}=\widehat{OBS}=90^0\)
hay SB là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C):
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C):
x
2
+
y
2
+
6
X
+
4
y
+
4
0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C'): x 2 + y 2 + 6 X + 4 y + 4 = 0 Tìm tâm vị tự của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) :
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C) :
x
2
+
y
2
+
6
x
+
4
y
+
4
0
Tìm tâm vị trí của hai đường tròn? A. I(0;1) và J(3;4) B. I(-1;-2) và J(3;2) C. I(1;2) và J(-3;-2) D. I(1;0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) : x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C') : x 2 + y 2 + 6 x + 4 y + 4 = 0 Tìm tâm vị trí của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
Cho đường tròn (C):
x
2
+
y
2
-
2
x
+
2
y
-
14
0
và đường thẳng ∆: - x + 2y – 2 0. Đường thẳng ∆ cắt đường tròn (C) theo dây cung có độ dài là: A.
11
B.
2
5
C.
2
11
D.
3
Đọc tiếp
Cho đường tròn (C): x 2 + y 2 - 2 x + 2 y - 14 = 0 và đường thẳng ∆: - x + 2y – 2 = 0. Đường thẳng ∆ cắt đường tròn (C) theo dây cung có độ dài là:
A. 11
B. 2 5
C. 2 11
D. 3