Hai tiếp tuyến tại B và C của nửa đường tròn (O;R) cắt nhau tại A. Biết OA = R. Tính số đo của cung BC.

Những câu hỏi liên quan
cho nửa đường tròn tâm O có đường kínhAB bằng 2r kẻ hai tiếp tuyến Ax By của nửa O tại A và B Ax By và nửa đường tròn O thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB qua điểm M thuộc nửa đường tròn M khác A B kẻ tiếp tuyến với nửa đường tròn cắt tia Ax By theo thứ tự tại C Da chứng minh AC + BD CD và tam giác BCD vuông tại Ob Tính tích AC nhân BD theo ABc các đường thẳng AB và BC cắt nhau tại N Chứng minh MN vuông góc với AB
Đọc tiếp
cho nửa đường tròn tâm O có đường kínhAB bằng 2r kẻ hai tiếp tuyến Ax By của nửa O tại A và B Ax By và nửa đường tròn O thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB qua điểm M thuộc nửa đường tròn M khác A B kẻ tiếp tuyến với nửa đường tròn cắt tia Ax By theo thứ tự tại C D
a chứng minh AC + BD = CD và tam giác BCD vuông tại O
b Tính tích AC nhân BD theo AB
c các đường thẳng AB và BC cắt nhau tại N Chứng minh MN vuông góc với AB
Cho nửa đường tròn (O) đường kính AB=2R. Lấy điểm M thuộc nửa đường tròn (O). Tiếp tuyến tại M cắt hai tiếp tuyến tại A và B của nửa đường tròn (O) lần lượt tại C và D.
a) Cm góc COD = 90 độ
b) Cm : CD = AC + BD
c) Cm AC.BD =\(R^2\)
MONG CÁC BẠN GIÚP MÌNH GIẢI CÂU NÀY!!
Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần lượt tại C và D.
b) Chứng minh AB tiếp xúc với đường tròn đường kính CD.
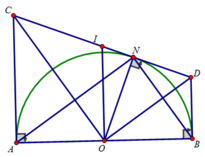
b) Gọi I là tâm của đường tròn đường kính CD.
Tứ giác CABD là hình thang vuông (AC ⊥ AB;BD ⊥ AB) có OI là đường trung bình
⇒ OI // AC ; mà AC ⊥ AB ⇒ OI ⊥ AB tại O
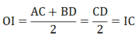
Vậy AB tiếp xúc với đường tròn đường kính CD.
Đúng 0
Bình luận (0)
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D a) COD là tam giác gì? b) C/m: CDAB+BD c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì? d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao? e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính di...
Đọc tiếp
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D a) COD là tam giác gì? b) C/m: CD=AB+BD c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì? d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao? e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tích của hình vuông này. Cho biết AB=6cm
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D
a) COD là tam giác gì?
b) C/m: CDAB+BD
c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?
d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?
e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tí...
Đọc tiếp
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D
a) COD là tam giác gì?
b) C/m: CD=AB+BD
c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?
d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?
e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tích của hình vuông này. Cho biết AB=6cm
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. (O và O’ nằm ở hai nửa mặt phẳng bờ AB). Một đường thẳng qua A cắt đường tròn (O) và (O’) tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai nửa đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE // KD (E thuộc BD).a) Chứng minh tam giác BOO’ và tam giác BCD đồng dạng.b) Chứng minh tứ giác BCKD nội tiếp.c) Chứng minh AE là tiếp tuyến của đường tròn (O; R).d) Tìm vị trí của CD để diện tích tam giác BCD lớn nhấ...
Đọc tiếp
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. (O và O’ nằm ở hai nửa mặt phẳng bờ AB). Một đường thẳng qua A cắt đường tròn (O) và (O’) tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai nửa đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE // KD (E thuộc BD).
a) Chứng minh tam giác BOO’ và tam giác BCD đồng dạng.
b) Chứng minh tứ giác BCKD nội tiếp.
c) Chứng minh AE là tiếp tuyến của đường tròn (O; R).
d) Tìm vị trí của CD để diện tích tam giác BCD lớn nhất.
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại Da) COD là tam giác gì?b) C/m: CDAB+BDc) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tí...
Đọc tiếp
Cho nửa đường tròn (o), đường kính AB. Hai tiếp tuyến Ax, By trên cùng 1 mặt phẳng bờ AB chứa nửa đường tròn (o). Tiếp tuyến tại điẻm M của nửa đường tròncắt Ax tại C và By tại D
a) COD là tam giác gì?
b) C/m: CD=AB+BD
c) AM và BM cắt OC và OD lần lượt tại E và F. Tứ giác OEMF là hình gì?
d) Gọi I là giao điểm 2 đường chéo OM và EF của tứ giác OEMF. Khi M thay đổi trên nửa đường tròn (o) thì điểm I chuyển động trên đường nào? Vì sao?
e) Xác định vị trí của M để tứ giác OEMF là hình vuông? Tính diện tích của hình vuông này. Cho biết AB=6cm
a: Xét (O) có
CM,CA là tiếp tuyến
nen CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là trung trực của AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của MB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
b: CD=CM+MD
=>CD=AC+BD
c: Xét tứ giác OEMF có
góc OEM=góc OFM=góc EOF=90 độ
nên OEMF là hình chữ nhật
Đúng 1
Bình luận (0)
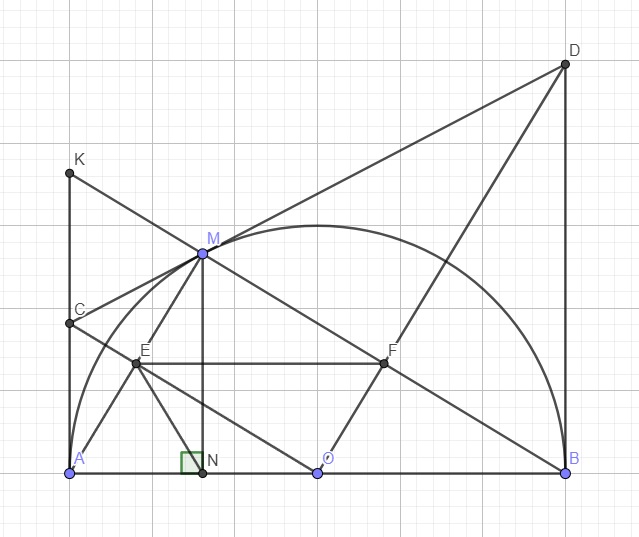
Cho nửa đường tròn (O;R) đường kính AB. Trên cùng một nửa mặt phẳng bờ AB chứa nửa đường tròn (O), vẽ hai tiếp tuyến Ax, By của nửa đường tròn. Từ điểm M thuộc nửa đường tròn (O) vẽ tiếp tuyến thứ ba cắt Ax, By lần lượt tại C và D. Tia BM cắt Ax tại K. Nối OC cắt AM tại E, nối OD cắt BM tại F.
- Kẻ MN vuông góc AB tại N. CM ONEF là hình thang cân.
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân
Đúng 1
Bình luận (2)
Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB.Từ điểm P trên Ax kẻ tiếp tuyến thứ hai PC với nửa đường tròn (C là tiếp điểm).AC cắt OP tại K; PB cắt nửa đường tròn (O) tại D (D khác B).
a.Chứng minh APDK la tứ giác nội tiếp đường tròn
b.Chứng minh góc ADK = góc ACO
Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
a) Chứng minh: AMDE là tứ giác nội tiếp đường tròn.
b) Chứng minh : góc ADE=góc ACO