m=abc,d;N=a,bcd
biết M+N=203,313
tính M-N
giúp em với
Những câu hỏi liên quan
5 tháng 10 2021 lúc 12:00
Cho tam giác ABC . d là trung trực của ABC , m là trung trực của BC . Chứng minh d cắt m tại 1 điểm.
Ta có: d là đường trung trực của tam giác ABC
m là đường trung trực BC
=> d cắt m tại giao điểm 3 đường trung trực tam giác ABC(hay còn gọi là tâm đường tròn ngoại tiếp tam giác)
Đúng 1
Bình luận (0)
Cho △ABC vuông tại A, góc ABC=60.BC=2a. Gọi M là trung điểm của BC, d là đường thẳng qua M và vuông góc với BC. Trên d lấy E phía ngoài tam giác ABC sao cho EM=AB. Chứng minh △BCE vuông.
Cho △ABC vuông tại A, góc ABC = 60.BC = 2a. Gọi M là trung điểm của BC, d là đường thẳng qua M và vuông góc với BC. Trên d lấy E phía ngoài △ABC sao cho EM=AB.( chỉ cần vẽ hình thôi )
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:16
Cho hình chóp S.ABC có SA \( \bot \) (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP),(ABC)) và d(NP,(ABC)).
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A,(SBC)).
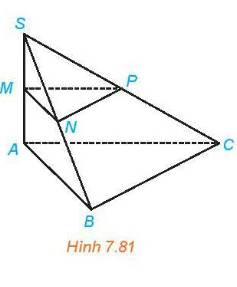
a) +) Xét tam giác SBC có
N, P lần lượt là trung điểm SB, SC
\( \Rightarrow \) PN là đường trung bình tam giác SBC
\( \Rightarrow \) PN // BC \( \Rightarrow \) PN // (ABC)
+) Xét tam giác SAB có
N, M lần lượt là trung điểm SB, SA
\( \Rightarrow \) MN là đường trung bình tam giác SAB
\( \Rightarrow \) MN // AB
+) \(\left. \begin{array}{l}PN//BC,MN//AB\\PN \cap MN = \left\{ N \right\},BC \cap AB = \left\{ B \right\}\end{array} \right\} \Rightarrow \left( {MNP} \right)//\left( {ABC} \right)\)
\( \Rightarrow \) d((MNP), (ABC)) = d(M, (ABC)) = MA \( = \frac{{SA}}{2} = \frac{h}{2}\) do SA \( \bot \) (ABC)
+) PN // (ABC) \( \Rightarrow \) d(NP,(ABC)) = d(N,(ABC)) = d(M,(ABC))\( = \frac{h}{2}\) (do MN // (ABC))
b)
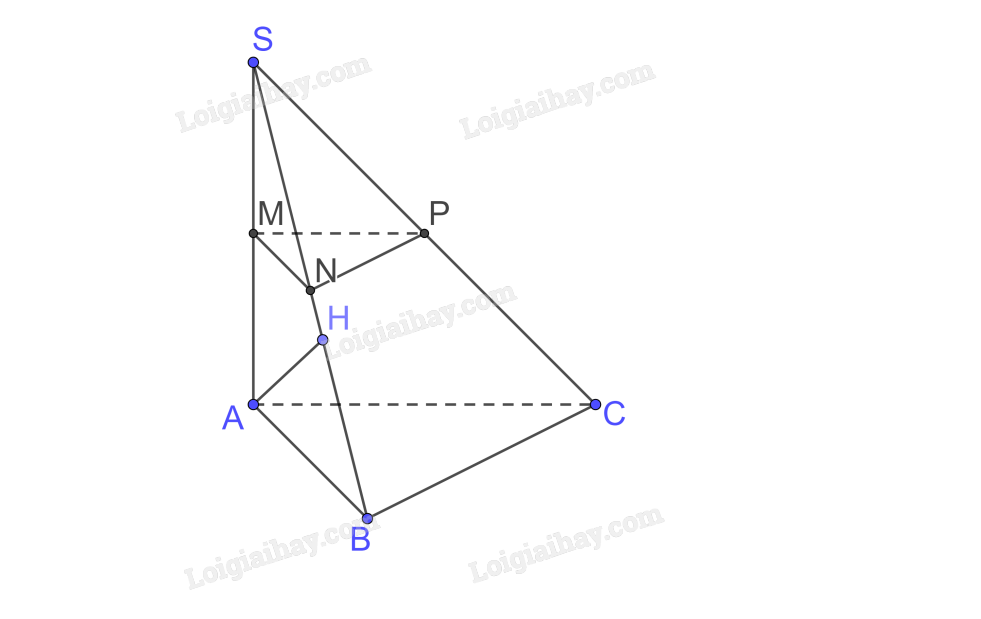
Ta có \(SA \bot BC,AB \bot BC \Rightarrow BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
\(\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
(SAB): kẻ \(AH \bot SB\)
\( \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow \) d(A,(SBC)) = AH
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{h^2}{a^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Đúng 0
Bình luận (0)
Cho tam giác đều ABC có cạnh bằng a. Đường thẳng d vuông góc với mp (ABC) tại A và \(M\in\left(d\right)\). Gọi H, O lần lượt là trực tâm của tam giác ABC và tam giác MBC. Gọi N là giao điểm của HO và d. Chứng minh tích AM.AN không đổi khi M thay đổi trên d ?
Cho tam giác ABC. Vẽ phân giác ngoài tại A của tam giác ABC. Từ B kẻ d//AD.
a) C/m: d cắt AC tại E.
b) C/m: góc ABE = góc AEB.
c) Từ B kẻ b vuông góc với AD, từ A kẻ a//b. C/m: b vuông góc với d và a là pg góc BAC.
a: d//AD
AD cắt AC tại A
Do đó: d cắt AC tại E
b: Gọi Ax là tia đối của tia AB
=>góc xAC là góc ngoài tại đỉnh A của ΔABC
=>AD là phân giác của góc xAC
AD//BE
=>góc xAD=góc ABE và góc DAE=góc AEB
mà góc xAD=góc DAE
nên góc ABE=góc AEB
c: b vuông góc AD
d//AD
Do đó: b vuông góc d
Đúng 1
Bình luận (0)
cho m=abc,d ;n=a,bcd.Biết m+n =203,313. Tinh m;n
ABC,D + A,BCD = 203,313
101. A,BCD = 203,313
A,BCD = 2,013
Vậy M - N = 201,3 - 2,013 = 199,287
Đúng 0
Bình luận (0)
abc,d+a,bdc=203,313
101.a,bcd=203,303
a,bcd=2,013
Vậy M-N = 201,32,013=199,287
ai 
mk mk lại thank you
Đúng 0
Bình luận (0)
Cho tam giác ABC , I là điểm nằm bên trong trong tam giác ABC D,E,F lần lượt là TĐ của BC,AC,AB gọi M,N,P là điểm đối xứng của I qua D,E,F
c/m tam giác ABC = tam giác MNP
Cho tạm giác ABC và trung tuyến AM. Đường thẳng d đi qua M( d không trùng với BC). Trên đường thẳng d lấy 2 điểm D và E sao cho M là trung điểm của DE.Gọi G là trọng tâm của tam giác ABC; N là trung điểm của AE. Chứng minh rằng 3 điểm D; G; N thẳng hàng
cho tam giác ABC,M là trung điểm của AB;D là trung điểm AC.Nối B với D,C với M và BD cắt CM tại O.Biết diện tích tam giác ABC bằng 48 cm2.Tính diện tích tam giác BOC.