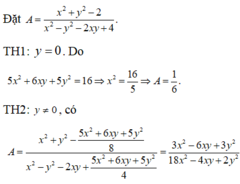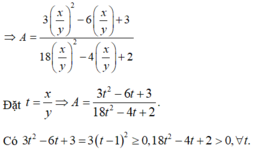Cho (d) y=(m-1)x + m2 + 4 Gọi A;B lần lượt là giao điểm của (d) với Ox và Oy xác định toạ độ A;B và tìm m để 3.OA=OB

Những câu hỏi liên quan
cho (d): y=(m-1)x + m2-4. gọi a,b lần lượt là giao điểm của (d) với ox và oy. xác định tọa độ a,b và tìm m để 3oa=ob
Bài hơi nhiều n cũng mong mn làm hết cho m . thanksBài 9:a, (x+3)(x+4)b,(x-4)(x2+4x+16)c,(xy2-1)(x2y+5)d,4(x-1/2)(x+1/2)(4x2+1)Bài 10:Cho biểu thức:P(m2-2m+4)(m+2)-m3+(m+3)(m-3)-m2 -18CM biểu thức P(x+y)3 -9(x+y)2 +27(x+y)-27ko thuộc vào mBài 11:a, (x2+2x+4)(2-x)+x(x-3)(x+4)-x2+240b, (x/2+3)(5-6x)+(12x-2)(x/4+3)0Bài 12: CM rằng với mọi x,y ta luôn có:(x4-x3y+x2y2-xy3+y4)(x+y)x5+y5Bài 13:Tìm 2 số lẻ liên tiếp , biết bình phương của số lớn, lớn hơn bình phương của số nhỏ là 80 đơn vịBài 14*:Cho a...
Đọc tiếp
Bài hơi nhiều n cũng mong mn làm hết cho m . thanks
Bài 9:
a, (x+3)(x+4)
b,(x-4)(x2+4x+16)
c,(xy2-1)(x2y+5)
d,4(x-1/2)(x+1/2)(4x2+1)
Bài 10:
Cho biểu thức:
P=(m2-2m+4)(m+2)-m3+(m+3)(m-3)-m2 -18
CM biểu thức P=(x+y)3 -9(x+y)2 +27(x+y)-27
ko thuộc vào m
Bài 11:
a, (x2+2x+4)(2-x)+x(x-3)(x+4)-x2+24=0
b, (x/2+3)(5-6x)+(12x-2)(x/4+3)=0
Bài 12:
CM rằng với mọi x,y ta luôn có:
(x4-x3y+x2y2-xy3+y4)(x+y)=x5+y5
Bài 13:
Tìm 2 số lẻ liên tiếp , biết bình phương của số lớn, lớn hơn bình phương của số nhỏ là 80 đơn vị
Bài 14*:
Cho a và b là 2 số tự nhiên thỏa mãn (a+3) và (b+4) cùng chia hết cho 5. CM a2+b2 cũng chia hết cho 5.
c)\(\left(xy^2-1\right)\left(x^2y+5\right)\)
\(=x^3y^3+5xy^2-x^2y-5\)
d)\(4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)\left(4x^2+1\right)\)
\(=4\left(x^2-\dfrac{1}{4}\right)\left(4x^2+1\right)\)
\(=4\left(4x^4+x^2-x-\dfrac{1}{4}\right)\)
\(=16x^4+4x^2-4x-1\)
Đúng 2
Bình luận (0)
Bài 9
a)\(\left(x+3\right)\left(x+4\right)\) b)\(\left(x-4\right)\left(x^2+4x+16\right)\)
\(=x^2+4x+3x+12\) \(=\left(x-4\right)\left(x^2+x.4+4^2\right)\)
\(=x^2+7x+12\) \(=x^3-4^3=x^3-64\)
Đúng 1
Bình luận (0)
bài 13
Tìm 2 số lẻ liên tiếp,biết bình phương số lơn lớn hơn bình phương số nhỏ là 80 đơn vị
2 số lẻ liên tiếp,biết bình phương số lơn lớn hơn bình phương số nhỏ là 80 đơn vị là :
19^2 và 21^2
Đúng 0
Bình luận (0)
Cho đường tròn (C) (x-1)2 + (y-1)2 = 25
(Cm) (x-2)2 + (y-m)2 = 16
Gọi m1, m2 là các giá trị thỏa mãn khoảng cách giữa hai giao điểm của C và Cm là lớn nhất Khẳng định nào sau đấy đúng
A. 1« m1 + m2 < 4
B. -1 « m1 + m2 <1
C. m1 + m2 » 4
D. m1 + m2 <-1
cho (d) y = ( m2 + 3m - 4 ) x -1 .
a) tìm m để (d) là hàm số bậc nhất b) ( d) đồng biến c) (d) nghịch biến
a: Để (d) là hàm số bậc nhất thì \(m^2+3m-4< >0\)
=>\(\left(m+4\right)\left(m-1\right)< >0\)
=>\(m\notin\left\{-4;1\right\}\)
b: Để (d) đồng biến thì \(m^2+3m-4>0\)
=>(m+4)(m-1)>0
=>m>1 hoặc m<-4
c: Để (d) nghịch biến thì m^2+3m-4<0
=>(m+4)(m-1)<0
=>-4<m<1
Đúng 0
Bình luận (0)
(P): y=x2 (d): y=2(m-1)x+m2+2m
CMR parabol (P) luôn cắt đường thẳng (d) tại 2 điểm phân biệt A,B .Gọi x1,x2 là hoành độ 2 điểm A,B tìm m sao cho:x12+x22+6x1x2>2016
Phương trình hoành độ giao điểm:
\(x^2=2\left(m-1\right)x+m^2+2m\Leftrightarrow x^2-2\left(m-1\right)x-m^2-2m=0\) (1)
\(\Delta'=\left(m-1\right)^2+m^2+2m=2m^2+1>0;\forall m\)
\(\Rightarrow\) (1) có 2 nghiệm pb với mọi m hay (P) luôn cắt (d) tại 2 điểm pb
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m^2-2m\end{matrix}\right.\)
\(x_1^2+x_2^2+6x_1x_2>2016\)
\(\Leftrightarrow\left(x_1+x_2\right)^2+4x_1x_2>2016\)
\(\Leftrightarrow\left(2m-2\right)^2+4\left(-m^2-2m\right)>2016\)
\(\Leftrightarrow-16m>2012\)
\(\Rightarrow m< -\dfrac{503}{4}\)
Đúng 0
Bình luận (0)
1. Cho d : y = (m2 + 2m)x + m + 1
Tìm m để :
a, d // d1 : y = (m + 6)x - 2
b, d ┸ d2 : y = -1/3x - 3
c, d ≡ d3 : y = -m2x + 1
2. Tìm d // d1 : y = -1/2x +1 và d đi qua giao điểm của d1 = 4x - 3 và d2 : y = -x +1
a: Để (d)//d1 thì \(\left\{{}\begin{matrix}m^2+m-6=0\\m+1\ne-2\end{matrix}\right.\Leftrightarrow m=2\)
Đúng 0
Bình luận (0)
Cho đường thẳng d: y (m − 1)x + m và d′: y
m
2
− 1)x + 6. Tìm m để đường thẳng d cắt trục tung tại A, d′ cắt trục hoành tại B sao cho tam giác OAB cân tại O A.
m
±
4
B.
m
±
2
C.
m
±
3
D.
m
±
1
Đọc tiếp
Cho đường thẳng d: y = (m − 1)x + m và d′: y = m 2 − 1)x + 6. Tìm m để đường thẳng d cắt trục tung tại A, d′ cắt trục hoành tại B sao cho tam giác OAB cân tại O
A. m = ± 4
B. m = ± 2
C. m = ± 3
D. m = ± 1
Cho đường thẳng d: y= (m-1) x+m và d’: y= (m2-1) x+ 6 . Tìm m để đường thẳng d cắt trục tung tại A, d’ cắt trục hoành tại B sao cho tam giác OAB cân tại O?
A. m= 2
B. m= -2
C. m= 1
D. Đáp án khác
Cho x,y thỏa mãn
5
x
2
+
6
x
y
+
5
y
2
16
và hàm số bậc ba y f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của
P
f
x
2
+
y...
Đọc tiếp
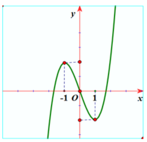
Cho x,y thỏa mãn 5 x 2 + 6 x y + 5 y 2 = 16 và hàm số bậc ba y = f(x) có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của P = f x 2 + y 2 - 2 x 2 - y 2 - 2 x y + 4 . Tính M 2 + m 2
![]()
![]()
![]()
![]()
Cho hàm số y=(m2-2m+3)x-4 (d) ,(với m là tham số)
1.Chứng minh rằng với mọi hàm số luôn đồng biến trên tập xác định của nó.
2.Tìm m để (d) đi qua A(2;8)
3.Tìm m để (d) song song với đường thẳng (d'):y=3x +m-4
2) Để (d) đi qua A(2;8) thì Thay x=2 và y=8 vào hàm số \(y=\left(m^2-2m+3\right)x-4\), ta được:
\(\left(m^2-2m+3\right)\cdot2-4=8\)
\(\Leftrightarrow2m^2-4m+6-4-8=0\)
\(\Leftrightarrow2m^2-4m-6=0\)
\(\Leftrightarrow2m^2-6m+2m-6=0\)
\(\Leftrightarrow2m\left(m-3\right)+2\left(m-3\right)=0\)
\(\Leftrightarrow\left(m-3\right)\left(2m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-3=0\\2m+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\2m=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=3\\m=-1\end{matrix}\right.\)
Vậy: Để (d) đi qua A(2;8) thì \(m\in\left\{3;-1\right\}\)
Đúng 1
Bình luận (0)