Cho tam giác ABC vuông tại A có AB=8cm;Ac=6cm
Trên AB lấy D sao cho AD=CA(D thuộc AB)
Trên tia đối của CA lấy E sao cho AE=AB(C thuộc AE)
Kẻ AH là đường cao của tam giác ABC.AH cắt DE tại M(M Thuộc DE)
CMR:AM là đường trung tuyến của tam giác ADE
1. Cho tam giác ABC vuông tại A, biết AH = 16, BH = 9. Tính AB.
2. Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính độ dài HB.
3. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12, BC = 15. Tính HC.
4. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 6, HC = 9. Tính độ dài AC.
5. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 12cm, BC = 16cm. Tính AH
6. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 8cm, HC = 12 cm. Tính AC.
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
a) Xét \(\Delta ABC\) vuông tại `A`
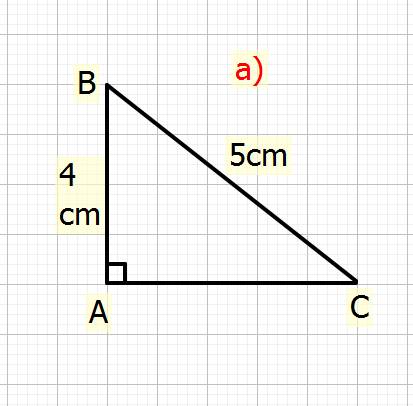
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
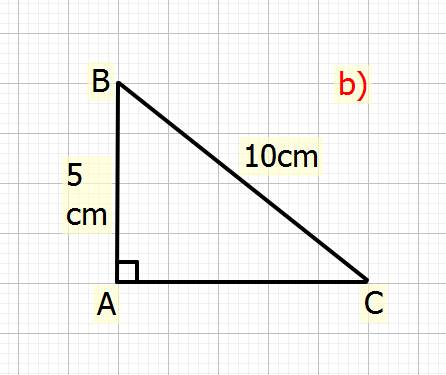
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
cho tam giác abc có ab=6cm,ac=8cm,bc=10cm. Kẻ ah vuông góc vs bc tại h 1 chứng minh tam giác abc vuông tại a 2 tính diện tích tam giác abc 3 tính AH
1) Ta có: \(BC^2=10^2=100\)
\(AB^2+AC^2=6^2+8^2=100\)
Do đó: \(BC^2=AB^2+AC^2\)(=100)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)
2) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
3) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm
Ta có: BC2=102=100
AB2+AC2=62+82=100
Vậy BC2=AB2+AC2
Xét ΔABC có:
BC2=AB2+AC2
Nên ΔABC vuông tại A(Định lí Pytago đảo)
Ta có: ΔABC vuông tại A(gt)
Nên
cho tam giác ABC có AB=8CM ; AC=6CM và BC=10CM . Chứng minh rằng tam giác ABC là tam giác vuông tại A
Ta có:
\(AB^2+AC^2=8^2+6^2=64+36=100\left(cm\right)\)
\(BC^2=10^2=100\left(cm\right)\)
\(\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A (định lý Pi-ta-go đảo)
Áp dụng định lý Pytago đảo ta có:
AB2+AC2=82+62=100
mà 102=100
⇒82+62=102hay AB2+AC2=BC2
vậy ABC là tam giác vuông tại A
áp dụng định lý pitago ta có :
ab^2+ac^2=8^2+6^2=100=10^2
=>bc=10cm
=>tam giác abc vuông tại a
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
b. So sánh các góc của tam giác ABC
b. Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A (quan hệ giữa góc và cạnh đối diện trong tam giác)
Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Vẽ đường cao AD của tam giác ABC. a) Chứng minh tam giác ABC vuông tại A và tam giác ABD đồng dạng tam giác CAD. b) Trên AB lấy điểm F sao cho AB = 3AF. Từ điểm D, vẽ đường thẳng vuông góc với FD tại D, đường thẳng này cắt AC tại E. Chứng minh: góc AFD = góc CED. c) Tính tỉ số:
a: Xét ΔABC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
Xét ΔABD vuông tại D và ΔCAD vuông tại D có
góc DBA=góc DAC
=>ΔABD đồng dạng với ΔCAD
b: góc EAF+góc EDF=180 độ
=>AFDE nội tiếp
=>góc AFD+góc AED=180 độ
=>góc AFD=góc CED
Cho tam giác ABC vuông tại A, AB=6cm, AC=8cm. Hãy giải tam giác vuông ABC
Xét tam giác ABC vuông tại A áp dụn Py-ta-go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-53^o\approx37^o\)
Xét \(\Delta ABC\)vuông tại A theo định lí Pitago ta có : \(AB^2+AC^2=BC^2\Rightarrow6^2+8^2=BC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét \(\Delta DEF\)vuông tại D theo định lí Pitago ta có :\(DE^2+DF^2=EF^2\)
=> \(DF^2=EF^2-DE^2=15^2-9^2=144\)
=> \(DF=\sqrt{144}=12\left(cm\right)\)
Để hai tam giác trên đồng dạng với nhau , trước hết tính tỉ lệ tương ứng với 3 cạnh
Xét tam giác ABC và tam giác DEF ta có :
\(\frac{AB}{DE}=\frac{6}{9}=\frac{2}{3}\)
\(\frac{BC}{EF}=\frac{10}{15}=\frac{2}{3}\)
\(\frac{AC}{DF}=\frac{8}{12}=\frac{2}{3}\)
=> \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\left(=\frac{2}{3}\right)\)
=> Tam giác ABC đồng dạng tam giác DEF
Nếu bạn muốn làm tam giác DEF đồng dạng với tam giác ABC cũng được
hai tam giác ko thể đồng dạng bạn nhé
Cho tam giác abc có AB=6cm;AC=8cm;Bc=10cm. chứng tỏ tam giác ABC vuông tại A,Tia phân giác của góc B cắt AC tại D, kẻ DE vuông góc với BC tại E
a) Ta có:
\(BC^2=AB^2+AC^2\)
\(10^2=6^2+8^2=36+64=100\)
Áp dụng định lí Pytago đảo
⇒ Tam giác ABC vuông tại A
b) 1/ Xét tam giác ABD và tam giác EBD có
^A=^E=90o(gt)
BD: cạnh chung
^B1=^B2(BD phân giác ^B)
⇒ Tam giác ABD= tam giác EBD
2/ Em xem lại đề ha
cho tam giác abc vuông tại A có AB = 6cm AC = 8cm a) tính BC b) tia phân giác của góc ABC cắt AC tại K kẻ KH vuông BC tại H
a: BC=10cm
b: Xét ΔABK vuông tại A và ΔHBK vuông tại H có
BK chung
\(\widehat{ABK}=\widehat{HBK}\)
Do đó: ΔABK=ΔHBK