Hệ thức lượng trong tam giác vuông
1) biết AH=30cm; AB/AC=5/6
Tính AB, AC,BC,HB,HC
2) biết BC= 125cm; AB/AC= 3/4
Tính HB, HC

Những câu hỏi liên quan
giúp em các cao thủ
Cho tam giác ABC vuông tại B , đường cao BH . Gọi M , N là hình chiếu của H trên AB , BC .
a) Viết các hệ thức lượng trong tam giác vuông AHB
b)Cho BC = 30cm , BH = 24cm ,Tính CH , AC , AH , AB .
c) Chứng minh : BN.BC + BM.BA = 2MN2
a: \(AB^2=HB^2+HA^2\)
\(BM\cdot BA=BH^2\)
\(AM\cdot AB=AH^2\)
\(BH\cdot HA=HM\cdot BA\)
\(HM^2=MA\cdot MB\)
c: Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHA vuông tại H có HM là đường cao ứng với cạnh huyền BA, ta được:
\(BM\cdot BA=BH^2\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBHC vuông tại H có HN là đường cao ứng với cạnh huyền BC, ta được:
\(BN\cdot BC=BH^2\)
Xét tứ giác BNHM có
\(\widehat{NBM}=\widehat{BNH}=\widehat{BMH}=90^0\)
Do đó: BNHM là hình chữ nhật
Suy ra: BH=NM
Ta có: \(BM\cdot BA+BN\cdot BC\)
\(=BH^2+BH^2\)
\(=2\cdot NM^2\)
Đúng 0
Bình luận (0)
Bạn tự vẽ hình nha.
a) \(sinA=\dfrac{BH}{AB},cosA=\dfrac{AH}{AB},tanA=\dfrac{BH}{AH},cotA=\dfrac{AH}{BH}\\sin \widehat{ABH}=\dfrac{AH}{AB},cos\widehat{ABH}=\dfrac{BH}{AB},tan\widehat{ABH}=\dfrac{AH}{BH},cot\widehat{ABH}=\dfrac{BH}{AH}\)
b)Áp dụng định lí Py-ta-go vào tam giác BHC vuông tại H, ta được:
\(CH=\sqrt{BC^2-BH^2}=\sqrt{900-576}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
\(AC=\dfrac{BC^2}{HC}=\dfrac{900}{18}=50\left(cm\right)\)
\(AB=\dfrac{BH\cdot AC}{BC}=\dfrac{24\cdot50}{30}=40\left(cm\right)\)
\(AH=\dfrac{AB^2}{AC}=\dfrac{400}{50}=8\)(cm)
c) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông, ta được:
BN.BC=\(BH^2\)
BM.BA=\(BH^2\)
Suy ra, BN.BC+BM.BA=2\(BH^2\)
Xét tứ giác BMHN có:
góc BMH = góc MBN = góc HNB = \(90^0\)
nên tứ giác BMHN là hình chữ nhật.
suy ra BH = MN .
Suy ra, BN.BC+BM.BA = 2.\(MN^2\)(đpcm)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A . AH là đường cao tính AH ; BC biết
a, AB = 6; Bc = 8
b, AB = 12 ; BC = 15
chú ý áp dụng hệ thức lượng trong tam giác vuông
Tam giác ABC vuông tại A có đường cao AH h và có BC a, CA b, AB c. Gọi BH c’ và CH b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:a2 b2 + (.....)b2 a x (.....)c2 a x (.....)h2 b’ x (.....)ah b x (.....)
Đọc tiếp
Tam giác ABC vuông tại A có đường cao AH = h và có BC = a, CA = b, AB = c. Gọi BH = c’ và CH = b’(h.2.11). Hãy điền vào các ô trống trong các hệ thức sau đây để được các hệ thức lượng trong tam giác vuông:
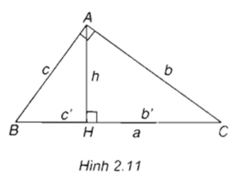
a2 = b2 + (.....)
b2 = a x (.....)
c2 = a x (.....)
h2 = b’ x (.....)
ah = b x (.....)
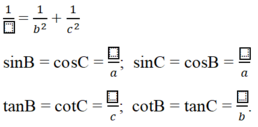
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c
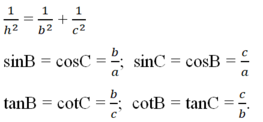
Đúng 1
Bình luận (0)
Toán Hệ thức lượng:
Tam giác ABC vuông tại A có AH là đường cao, AH=12cm, AB= 3/5BC. Tính chu vi tam giác ABC?
BÀI 1 – HỆ THỨC GIỮA CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNGI . MỨC ĐỘ NHẬN BIẾT.Câu 1. _NB_ Cho tam giác ABC vuông tại A , đường cao AH . Hệ thức nào sau đây làđúng?A. AH AB.AC 2 . B. AH BH.CH 2 .C. AH AB.BH 2 . D. AH CH.BC 2 .Câu 2. _NB_ Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng … .Điền cụm từ thích hợp vào chỗ trống:A. Tích hai cạnh góc vuông.B. Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.C. Tích cạnh huyền và 1 cạnh góc vuông.D. Tổng nghịch đảo các bìn...
Đọc tiếp
BÀI 1 – HỆ THỨC GIỮA CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
I . MỨC ĐỘ NHẬN BIẾT.
Câu 1. _NB_ Cho tam giác ABC vuông tại A , đường cao AH . Hệ thức nào sau đây là
đúng?
A. AH AB.AC 2 . B. AH BH.CH 2 .
C. AH AB.BH 2 . D. AH CH.BC 2 .
Câu 2. _NB_ "Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng … ".
Điền cụm từ thích hợp vào chỗ trống:
A. Tích hai cạnh góc vuông.
B. Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
C. Tích cạnh huyền và 1 cạnh góc vuông.
D. Tổng nghịch đảo các bình phương của hai cạnh góc vuông.
Câu 3. _NB_ Cho tam ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào sau
đây là sai ?
A. b b .a 2 . B.
2 2 2
1 1 1
h c b
. C. a.h b .c . D. h b .c 2 .
Câu 4. _NB_ Cho tam giác ABC vuông tại A , đường cao AH (như hình vẽ). Hệ thức nào
sau đây là sai?
A. AB BH.BC 2 . B. AC CH.BC 2 .
c b
h
c' b'
a
H C
A
B
B H C
A
C. AB.AC AH.BC . D.
2 2
2
2 2
AB AC
AH
AB .AC
.
Câu 5. _NB_ Cho tam giác ABC , đường cao AH . Câu nào sau đây là đúng?
A. AB AC BC 2 2 2 . B. AH BH.CH 2 .
C. AB BH.BC 2 . D. Cả A, B, C đều sai.
Câu 6. _NB_ Cho tam giác ABC , đường cao AH . Hệ thức nào dưới đây chứng tỏ ABC
vuông tại A ?
A. BC AB AC 2 2 2 . B. AH BH.CH 2 .
C. AB BH.BC 2 . D. AC CH.BC 2 .
Câu 7. _NB_ Cho ABC có A C 90o và BH là đường cao. Câu nào sau đây đúng?
A.
2 2 2
1 1 1
AH AB AC
. B. AH HB.HC 2 .
C.
2 2 2
1 1 1
BH AB BC
. D. AB HB.BC 2 .
Câu 8. _NB_ Cho ABC vuông tại A có đường cao AH ( H thuộc cạnh BC ). Hình chiếu
của
H trên AB là E , trên AC là F . Câu nào sau đây đúng?
A. AH AE.AB 2 . B. AH AF.AC 2 .
C. AB.AE AC.AF . D. Cả A, B, C đều đúng.
II. MỨC ĐỘ THÔNG HIỂU.
Câu 9. _TH_ Giá trị của x,y trong hình vẽ sau là
A. x 6,5; y 9,5 . B. x 6,25; y 9,75.
C. x 9,25; y 6,75. D. x 6; y 10 .
Câu 10. _TH_ Giá trị của x,y trong hình vẽ sau là
10
x y
16
B H C
A
A. x 3,6; y 6,4 . B. x 6,4; y 3,6 .
C. x 4; y 6 . D. x 2,8; y 7,2 .
Câu 11. _TH_ Giá trị của x trong hình vẽ sau là
A. x 14 . B. x 13. C. x 12. D. x 145 .
Câu 12. _TH_ Giá trị của x, y trong hình vẽ sau là
A. x ; y 74 35 74
74
. B. x 74; y 35 74
74
.
C. x 4; y 6 . D. x 2,8; y 7,2 .
Câu 13. _TH_ Giá trị của x trong hình vẽ sau là
x y
8
6
H
B C
A
x
20
15
H
C
B
A
5 7
x
y
B H C
A
A. x 6 2 . B. x 8 2 . C. x 8 3 . D. x 8
2
.
Câu 14. _TH_ Giá trị của x trong hình vẽ sau là
A. x 6,4 . B. x 4,8 . C. x 4 . D. x 2,8 .
III. MỨC ĐỘ VẬN DỤNG.
Câu 15. _VD_ Cho ABCD là hình thang vuông tại A và D . Đường chéo BD vuông góc với
BC . Kẻ đường cao BE E DC . Biết AD=12cm , DC=25cm . Tính độ dài BC ,
biết BC 20 .
A. BC=15cm . B. BC=16 cm . C. BC=14cm . D.
BC=17 cm.
Câu 16. _VD_ Cho tam giác ABC vuông tại A , đường cao AH . Cho biết AB : AC 5 :7 và
AH =15cm . Độ dài đoạn thẳng CH là
A. CH =36 cm . B. CH =21cm. C. CH =25cm . D.
CH =27 cm .
Câu 17. _VD_ Cho tam giác ABC vuông tại A , đường cao AH . Biết AB : AC 5 :12 và
AB+ AC=34cm . Tính các cạnh của tam giác ABC .
A. AB=5cm ; AC=12cm; BC=13cm .
B. AB=24cm ; AC=10cm ; BC=26 cm .
C. AB=10cm ; AC=24cm ; BC=26 cm .
D. AB=26 cm ; AC=12cm; BC=24cm .
Câu 18. _VD_ Cho tam giác ABC vuông tại A , đường cao AH . Biết AB : AC 5 :12 và
x x
8
D
N P
M
x
8
6
B H C
A
AB+AC=34cm . Tính độ dài các đoạn AH, BH, CH AH,BH,CH (làm tròn đến
chữ số thập phân thứ hai).
A. AH 9,23cm ; BH 3,85cm; CH 22,15cm .
B. AH 9,3cm ; BH 3,9cm ; CH 22,2 cm .
C. AH 9,23cm ; BH 3,84cm ; CH 22,15cm .
D. AH 3,85cm ; BH 9,23cm ; CH 22,15cm .
IV. MỨC ĐỘ VẬN DỤNG CAO.
Câu 19. _VDC_ Cho tam giác ABC vuông tại A , đường cao AH . Gọi D và E lần lượt là
hình chiếu vuông góc của H trên AB,AC ( hình vẽ). Tỉ số
3 3
AB
AC
bằng với tỉ số nào
sau đây?
A.
3 3
AB BD
AC EC
. B.
3 3
AB AD
AC EC
. C.
3 3
AB BD
AC ED
. D.
3 3
AB EC
AC BD
.
Câu 20. _VDC_ Cho tam giác ABC vuông tại A , đường cao AH . Cho biết BH=4cm ;
CH=9cm . Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và
AC . Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại
M , N (hình vẽ). Tính diện tích tứ giác DENM .
A. cm2
S =19,5 DENM . B. S =20,5 DENM cm2 . C. S =19 DENM cm2 . D.
cm2
S =21,5 DENM .
M N
D
E
H C
A
B
Cho tam giác ABC vuông tại A c/m hệ thức lượng trong tam giác vuông: h ²= b' × c' ( Trong đó AH là đường cao(h), BH là hình chiếu của AB lên BC (c'), CH là hình chiếu của AC lên BC (b')
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB = 10cm , AH=6cm.
tinh do dai canh AC.BC cua tam giac ABC
lưu ý: sử dụng các hệ thức cạch và đường cao trong tam giác vuông
+) Xét tam giác ABC vuông tại A có AH là đường cao => AH là đường trung tuyến của tam giác ABC
=> AH=BH=CH=\(\frac{1}{2}BC\)=6 cm
=> BC=12cm
+) Xét tam giác ABC vuông tại A theo định lí pitago có:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow10^2+AC^2=12^2\Leftrightarrow AC=\sqrt{44}\)
Vậy AC=\(\sqrt{44}\)
chúc bn học tốt!
cho tam giác abc vuông tại a biết ac =18cm bc=30cm a)giải tam giác vuông b)kẻ đường cao AH. Tính CH, BH, AH
a, \(AB=\sqrt{BC^2-AC^2}=24\left(cm\right)\left(pytago\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}=90^0-\widehat{B}\approx53^0\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=19,2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=10,8\left(cm\right)\\AH=\sqrt{BH\cdot CH}=14,4\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (1)
PHẦN B. HÌNH HỌC Bài 1. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 1. BÀI TẬP CƠ BẢN AB=5cm;BC=1dm
tính lần lượt độ dài các đoạn bc,ch,ah,ac
Xét tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}\)
\(\Rightarrow AB=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AH^2=\dfrac{AC^2AB^2}{AC^2+AB^2}\)
\(\Rightarrow AH=\sqrt{\dfrac{AC^2AB^2}{AC^2+AB^2}}\)
\(\Rightarrow AH=\sqrt{\dfrac{\left(5\sqrt{3}\right)^2\cdot5^2}{\left(5\sqrt{3}\right)^2+5^2}}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Áp dụng hệ thưcs cạnh góc vuông và hình chiếu ta có:
\(\left\{{}\begin{matrix}AB^2=BC\cdot BH\\AC^2=BC\cdot CH\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{5^2}{10}=2,5\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{\left(5\sqrt{3}\right)^2}{10}=7,5\left(cm\right)\end{matrix}\right.\)
Đúng 4
Bình luận (0)


















