viết phương trình các cạnh của tam giác ABC biết A(2;2) và 2 đường cao d1: x+y-2=0, d2:9x-3y+4=0

Những câu hỏi liên quan
Cho tam giác ABC đều có A(2; 0) phương trình BC: \(\sqrt{3}x-3y+6=0\). Viết phương trình các cạnh còn lại của tam giác ABC.
Đường thẳng BC nhận \(\overrightarrow{n}=\left(\sqrt{3};-3\right)\) là 1 vtpt
Gọi \(\overrightarrow{n_1}=\left(a;b\right)\) là 1 vtpt của AB (với a;b không đồng thời bằng 0)
Do tam giác ABC đều \(\Rightarrow\widehat{\left(n_1;\overrightarrow{n}\right)}=60^0\)
\(\Rightarrow cos\left(\overrightarrow{n_1};\overrightarrow{n}\right)=\dfrac{\left|a\sqrt{3}-3b\right|}{\sqrt{a^2+b^2}.\sqrt{3+9}}=\dfrac{1}{2}\)
\(\Leftrightarrow\left(a-\sqrt{3}b\right)^2=a^2+b^2\)
\(\Leftrightarrow a^2+3b^2-2\sqrt{3}ab=a^2+b^2\)
\(\Leftrightarrow b^2=\sqrt{3}ab\Rightarrow\left[{}\begin{matrix}b=0\\b=\sqrt{3}a\end{matrix}\right.\)
\(\Rightarrow\) Phương trình 2 cạnh còn lại có dạng:
\(\left\{{}\begin{matrix}a\left(x-2\right)+0\left(y-0\right)=0\\a\left(x-2\right)+\sqrt{3}a\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\x+\sqrt{3}y-2=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho tam giác ABC có phương trình đường thẳng chứa cạnh AB là 5x - 3y + 2 = 0,và các đường cao kể từ A,B lần lượt có phương trình 4x - 3y + 1 = 0 và 7x + 2y - 22 = 0. viết phương trình các cạnh còn lại của tam giác ABC
Cho tam giác ABC có phương trình các cạnh AB. x+y-1 0; AC: 7x- y+20 và BC: 10x+ y-190. Viết phương trình đường phân giác trong góc A của tam giác ABC. A. 12x+ 4y-3 0 B. 2x-6y+7 0 C. 12x+ 6y+ 5 0 D. 2x+6y-70
Đọc tiếp
Cho tam giác ABC có phương trình các cạnh AB. x+y-1= 0; AC: 7x- y+2=0 và BC: 10x+ y-19=0. Viết phương trình đường phân giác trong góc A của tam giác ABC.
A. 12x+ 4y-3= 0
B. 2x-6y+7= 0
C. 12x+ 6y+ 5= 0
D. 2x+6y-7=0
Đáp án B
Do AB và BC cắt nhau tại B nên toa độ điểm B là nghiệm hệ phương trình

Do đó: B( 2; -1)
Tương tự: tọa độ điểm C( 1; 9)
PT các đường phân giác góc A là:
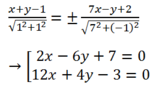
Đặt T1(x; y) = 2x- 6y+ 7 và T2= 12x+ 4y-3 ta có:
T1(B). T1(C) < 0 và T2(B) T2(C) >0.
Suy ra B và C nằm khác phía so với đường thẳng 2x-6y+7= 0 và cùng phía so với đường thẳng: 12x+ 4y- 3= 0.
Vậy phương trình đường phân giác trong góc A là: 2x- 6y+ 7= 0.
Đúng 0
Bình luận (0)
Cho tam giác ABC với A(-1;-2) và phương trình đường thẳng chứa cạnh BC là xy+4=0. a) Viết phương trình đường cao AH của tam giác. b) Viết phương trình đường trung bình ứng với cạnh đáy BC của tam giác.
a: BC: x+y+4=0
=>AH: -x+y+c=0
Thay x=-1 và y=-2 vào AH, ta được:
c+1-2=0
=>c=1
=>-x+y+1=0
=>x-y-1=0
b: BC: x+y+4=0
=>B(x;-x-4)
Tọa độ M là:
xM=(x-1)/2 và yM=(-x-4-2)/2=(-x-6)/2
BC: x+y+4=0
=>MN: x+y+c=0
Thay xM=(x-1)/2 và yM=(-x-6)/2 vào MN, ta được:
\(\dfrac{x-1}{2}+\dfrac{-x-6}{2}+c=0\)
=>c+(1/2x-1/2-1/2x-3)=0
=>c=7/2
=>x+y+7/2=0
Đúng 1
Bình luận (0)
Trên mặt phẳng tọa độ cho A(1;1) B(-2;-3) C(2;-1)
a) viết các phương trình đường thẳng chứa các cạnh của tam giác ABC
b)tìm tọa độ đỉnh D của hình bình hành ABCD
c)tam giác ABC là tam giác gì?tính Sabc
d)viết các phương trình đường trung trực của BC
e)viết các phương trình đường thẳng đi qua A và song song với BC
trong mặt phẳng Oxy cho A(2,1) , B(-1,2) , C(3,-1) : a) viết phương trình các cạnh AB , BC , AC ; b) viết phương trình các đường cao kẻ từ các đỉnh A , B , C của tam giác ABC ; c) viết phương trình các đường trung tuyến kẻ từ các đỉnh A , B , C của tam giác ABC
trong mặt phẳng Oxy cho A(2;1) , B(-1;2) , C(3;-1) : a) viết phương trình các cạnh AB , BC .AC ; b) viết phương trình các đường cao kẻ từ các đỉnh A , B , C của tam giác ABC ; c) viết phương trình các đường trung tuyến kẻ từ các đỉnh A , B , C của tam giác ABC
a: (d): 2x-y+3=0
=>y=2x+3
Vì (d') vuông góc với (d) nên 2a=-1
=>a=-1/2
Vậy: (d'): y=-1/2x+b
Thay x=3 và y=1 vào (d'), ta được:
b-3/2=1
hay b=5/2
Vậy: (d'): y=-1/2x+5/2
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-\dfrac{1}{2}x+\dfrac{5}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-\dfrac{1}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=-\dfrac{2}{5}+3=\dfrac{13}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
trong mặt phẳng Oxy cho A(2;1) , B(-1;2) , C(3;-1) : a) viết phương trình các cạnh AB , BC .AC ; b) viết phương trình các đường cao kẻ từ các đỉnh A , B , C của tam giác ABC ; c) viết phương trình các đường trung tuyến kẻ từ các đỉnh A , B , C của tam giác ABC .
trong mặt phẳng Oxy cho A(2,1) , B(-1,2) , C(3,-1) : a) viết phương trình các cạnh AB , BC , AC ; b) viết phương trình các đường cao kẻ từ các đỉnh A , B , C của tam giác ABC ; c) viết phương trình các đường trung tuyến kẻ từ các đỉnh A , B , C của tam giác ABC




















