Cho điểm M(5;2) và đường thẳng (d): 3x – y + 2 = 0. Tìm ảnh của M qua phép đối xứng qua đường thẳng (d)
A. (–5;4)
B. (5;4)
C. (4;5)
D. (–4;5)
Những câu hỏi liên quan
Cho hai điểm A(2; 4) và M(5 ; 7). Tìm toạ độ điểm B sao cho M là trung điểm đoạn thẳng AB.
Giả sử B có tọa độ: \(B\left( {{x_B},{y_B}} \right)\)
Do M là trung điểm của đoạn thẳng AB nên: \(\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_B}}}{2}\\{y_M} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_A}\\{y_B} = 2{y_M} - {y_A}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 2.5 - 2 = 8\\{y_B} = 2.7 - 4 = 10\end{array} \right.\)
Vậy tọa độ điểm B là: \(B\left( {8;10} \right)\)
Đúng 0
Bình luận (0)
Giả sử B có tọa độ: \(B\left(x_B,y_B\right)\)
Do M là trung điểm của đoạn thẳng AB nên:
\(\left\{{}\begin{matrix}x_M=\dfrac{x_A+x_B}{2}\\y_M=\dfrac{y_A+y_B}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=2x_M-x_A\\y_B=2y_M-y_A\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B=2.5-2=8\\y_{B=}=2.7-4=10\end{matrix}\right.\)
Đúng 0
Bình luận (6)
cho 4 điểm M ,N ,P ,Q sao cho : điểm N nằm giữa 2 điểm M và P ; ba điểm M, N, Q không thẳng hàng . Số các đường thẳng phân biệt đi qua ít nhất hai điểm đã cho là ?
A .3 B.4 C.5 D.6
1 Cho đoạn thẳng AB , C là một điểm thuộc đoạn thẳng AB . Gọi M,N lần lượt là trung điểm của AC và CBCho biết ACCB và I là trung điểm MN. Ba điểm M,C,I điểm nào nằm giữa hai điểm còn lại2 Cho 5 điểm a.Có bao nhiêu đoạn thẳng qua 5 điểm đó b.Cho đường thẳng a ko đi qua bất kì điểm nào trong 5 điểm đó.Chứng tỏ a ko thể cắt đc 5 đoạn thẳng đc tạo thành từ 5 điểm đó
Đọc tiếp
1 Cho đoạn thẳng AB , C là một điểm thuộc đoạn thẳng AB . Gọi M,N lần lượt là trung điểm của AC và CB
Cho biết AC<CB và I là trung điểm MN. Ba điểm M,C,I điểm nào nằm giữa hai điểm còn lại
2 Cho 5 điểm
a.Có bao nhiêu đoạn thẳng qua 5 điểm đó
b.Cho đường thẳng a ko đi qua bất kì điểm nào trong 5 điểm đó.Chứng tỏ a ko thể cắt đc 5 đoạn thẳng đc tạo thành từ 5 điểm đó
Cho 3 điểm M , N , O . Vẽ OM = 2, 8 cm , MN =5, 5 cm , ON = 3,2 cm . Chứng tỏ rằng
Trong 3 điểm M,N,O không có điểm nằm giữa 2 điểm còn lại.
Ba điểm M,N ,O không thẳng hàng
Cho điểm M(1;2) và đường thẳng d: 2x+ y- 5 0. Toạ độ của điểm đối xứng với điểm M qua d là:
Đọc tiếp
Cho điểm M(1;2) và đường thẳng d: 2x+ y- 5= 0. Toạ độ của điểm đối xứng với điểm M qua d là:
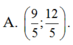
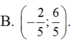
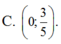
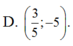
Đáp án A
Ta thấy: M ∉ d
Gọi H( a; b) là hình chiếu của điểm M lên đường thẳng d.
Ta có đường thẳng d có vtpt: n → = ( 2 ; 1 )
Suy ra u → ( - 1 : 2 ) là vectơ chỉ phương của đường thẳng d.
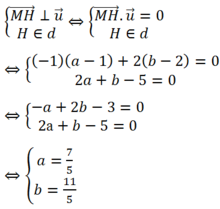
Do đó: H 7 5 ; 11 5
Gọi M’(x; y) đối xứng với M qua đường thẳng d. Khi đó ; H là trung điểm của MM’
Ta có:
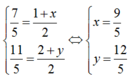
Vậy tọa độ điểm đối xứng với M qua d là: M ' ( 9 5 ; 12 5 )
Đúng 0
Bình luận (0)
Cho điểm M(1;2) và đường thẳng d: 2x + y - 5 0. Toạ độ của điểm đối xứng với điểm M qua d là: A. (
9
5
;
12
5
) B. (
-
2
5
;
6
5
) C. (
0
;
3
5
) D. (
3
5
;
-
5
)
Đọc tiếp
Cho điểm M(1;2) và đường thẳng d: 2x + y - 5 = 0. Toạ độ của điểm đối xứng với điểm M qua d là:
A. ( 9 5 ; 12 5 )
B. ( - 2 5 ; 6 5 )
C. ( 0 ; 3 5 )
D. ( 3 5 ; - 5 )
Chọn A.
Ta thấy M ∉ d.
Gọi H(a,b) là hình chiếu của điểm M lên đường thẳng d.
Ta có đường thẳng d: 2x + y - 5 = 0 nên có vtpt: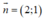 
Suy ra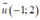 
là vectơ chỉ phương của đường thẳng d
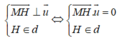
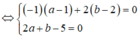
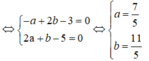
Do đó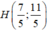 
Gọi M'(x,y) đối xứng với M qua đường thẳng d. Khi đó, H là trung điểm của MM'
Ta có:
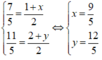
Vậy tọa độ điểm đối xứng với M qua d là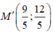 
Đúng 0
Bình luận (0)
Cho 5 điểm A, B, C, M, N cùng thuộc một đường thẳng sao cho điểm C nằm giữa A và B, điểm M nằm giữa A và C, điểm N nằm giữa C và B
tìm m để đồ thị hàm số y= 2x +m+5 (m là tham số ) cắt trục tung tại điểm A, cắt trục hoành tại điểm B sao cho AB bằng căn 5.. cíuuu
Lời giải:
$A$ thuộc trục tung nên $x_A=0$
$y_A=2x_A+m+5=2.0+m+5=m+5$. Vậy $A(0,m+5)$
$B$ thuộc trục hoành nên $y_B=0$
$0=y_B=2x_B+m+5$
$\Rightarrow x_B=\frac{-m-5}{2}$
Vậy $B(\frac{-m-5}{2},0)$
\(AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2}=\sqrt{5}\)
$\Leftrightarrow (x_A-x_B)^2+(y_A-y_B)^2=5$
$\Leftrightarrow (0-\frac{-m-5}{2})^2+(m+5-0)^2=5$
$\Leftrightarrow \frac{(m+5)^2}{4}+(m+5)^2=5$
$\Leftrightarrow (m+5)^2=4\Leftrightarrow m+5=\pm 2$
$\Rightarrow m=-3$ hoặc $m=-7$
Đúng 2
Bình luận (0)
cho điểm M (-3 , 5) . hãy chỉ rõ hoành độ và tung độ của điểm M
hoành độ:-3
tung độ :5
hok tốt nha ^_^
░░░░░░░░░░░░▄▄
░░░░░░░░░░█░░░█
███████▄▄█░░░░░██████▄
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█░░░░░░░░░░░░░░█
▓▓▓▓▓▓█████░░░░░░░░░█
██████▀░░░░▀▀██████▀
Đúng 0
Bình luận (0)
Câu 4: Khẳng định đúng trong các khẳng định sau là
A. -3/5 < -14/5 B.-7/-9 > 0 C.11/10 < 11/15 D.-30/29 > 9/29
Câu 5: Cho hai tia đối OA và OB,M lag một diểm thuộc tia OA.Trong ba điểm M,O,B điểm nào nào giữa hai điểm còn lại?
A. Điểm M B. Điểm A C. Điểm O D. Điểm B
Câu 6: Trong các cách viết sau cách viết nào ko phải là phân số ?
A.9 B.0/7 C. 3,2/19 D.-8/15
