Trong mặt phẳng Oxy, một trong các đường thẳng đi qua E\(\left(\frac{7}{3};-2\right)\) và cách M(1;2) một khoảng là 4 có dạng Ax+By-15=0. Tính A+B

Những câu hỏi liên quan
Trong mặt phẳng Oxy, một trong các đường thẳng đi qua E\(\left(\frac{7}{3};-2\right)\) và cách M(1;2) một khoảng là 4 có dạng Ax+By-15=0. Tính A+B
Trong mặt phẳng Oxy, một trong các đường thẳng đi qua E\(\left(\frac{7}{3};-2\right)\) và cách M(1;2) một khoảng là 4 có dạng Ax+By-15=0. Tính A+B
Xem chi tiết
\(\left\{{}\begin{matrix}d\left(M;d\right)=4\\\frac{7}{3}A-2B-15=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\frac{\left|A+2B-15\right|}{\sqrt{A^2+B^2}}=4\\7A-6B-45=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(A+2B-15\right)^2=16A^2+16B^2\\7A-6B-45=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}A^2-3A=0\\B=\frac{7A-45}{6}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}A=0;B=-\frac{15}{2}\\A=3;B=-4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy,đường thẳng d đi qua M(-2;3) và song song với đường thẳng EF.Biết E(0;-1),F(-3;0).Viết phương trình đường thẳng d
\(\overrightarrow{EF}=\left(-3;1\right)\)
Do d song song EF nên d nhận (1;3) là 1 vtpt
Phương trình d:
\(1\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-7=0\)
Đúng 1
Bình luận (1)
Câu 2. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d1):y=x+2 (d2):y=-x+4 và (d_{3}):y=mx+m. (m là tham số thục). a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ Oxy. b) Xác định các giá trị của tham số m để đường thẳng (d3) đi qua giao điểm của (d1)và(d2)
a: 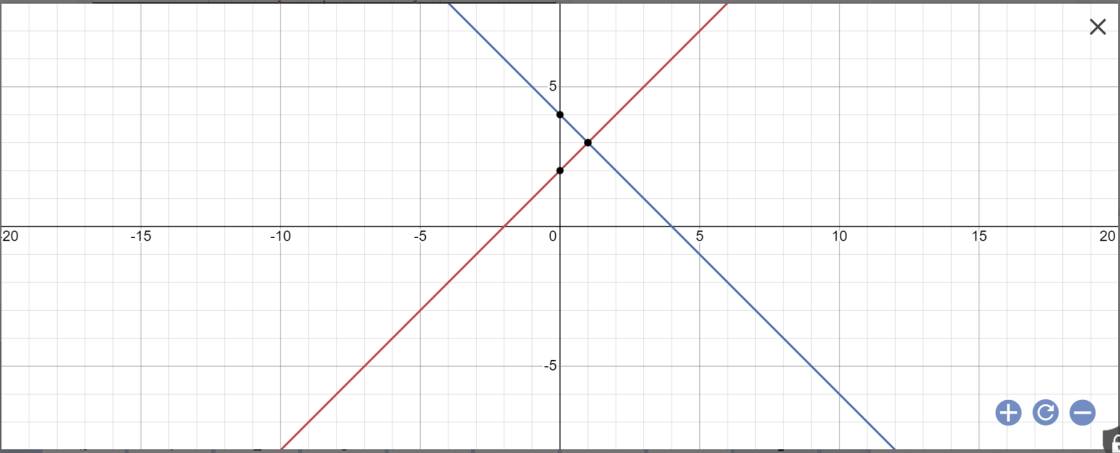
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho tứ giác ABCD nội tiếp trong đường tròn đường kính BD. Gọi H, K lần lượt là hình chiếu vuông góc của điểm A trên các đường thẳng BC, BD và E là giao điểm của hai đường thẳng HK và AC. Biết đường thẳng AC đi qua điểm M(3;2) và nhận overrightarrow{n} (1;-1) làm vectơ pháp tuyến. Tìm tọa độ các điểm E và A, biết điểm H(1;3), K(2;2) và hoành độ điểm A lớn hơn 2.Help me!!!Thanks trc
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho tứ giác ABCD nội tiếp trong đường tròn đường kính BD. Gọi H, K lần lượt là hình chiếu vuông góc của điểm A trên các đường thẳng BC, BD và E là giao điểm của hai đường thẳng HK và AC. Biết đường thẳng AC đi qua điểm M(3;2) và nhận \(\overrightarrow{n}\) = (1;-1) làm vectơ pháp tuyến. Tìm tọa độ các điểm E và A, biết điểm H(1;3), K(2;2) và hoành độ điểm A lớn hơn 2.
Help me!!!
Thanks trc
Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại C, có phân giác AD với Dleft(dfrac{7}{2};-dfrac{7}{2}right) thuộc BC. Gọi E, F lần lượt thuộc các cạnh AB, AC sao cho AEAF. Đường thẳng EF cắt BC tại K. Biết Eleft(dfrac{3}{2};-dfrac{5}{2}right), F có hoành độ nhỏ hơn 3 và phương trình đường thẳng AK là x-2y-30. Viết phương trình các cạnh tam giác ABC.
Đọc tiếp
Trong mặt phẳng với hệ trục Oxy, cho tam giác ABC vuông tại C, có phân giác AD với \(D\left(\dfrac{7}{2};-\dfrac{7}{2}\right)\) thuộc BC. Gọi E, F lần lượt thuộc các cạnh AB, AC sao cho \(AE=AF\). Đường thẳng EF cắt BC tại K. Biết E\(\left(\dfrac{3}{2};-\dfrac{5}{2}\right)\), F có hoành độ nhỏ hơn 3 và phương trình đường thẳng \(AK\) là \(x-2y-3=0\). Viết phương trình các cạnh tam giác ABC.
Từ hình vẽ thì hướng giải như sau:
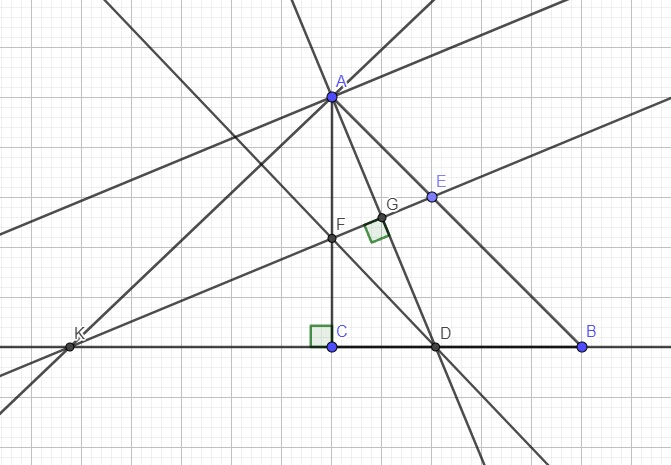
Dễ dàng nhận ra \(DF\perp AK\), từ đó biết vtpt của DF \(\Rightarrow\) phương trình DF
\(\Rightarrow\) Tọa độ F (là giao của DF và đường tròn tâm D bán kính DE do DE=DF)
Biết tọa độ F \(\Rightarrow\) viết được pt AD qua D vuông góc EF
\(\Rightarrow\) Tọa độ A từ là giao AK và AD
\(\Rightarrow\) Phương trình AB qua A và E, phương trình AC qua A và F, phương trình BC qua D và vuông góc AF
Đúng 3
Bình luận (0)
2. Trong mặt toạ độ Oxy , cho đg thẳng d x =3 -2t ; y = 1+3t. Một vectơ chỉ phương của đg thẳng d là?
7. Trong mặt phẳng toạ độ Oxy , viết pt tham số của đg thẳng d đi qua điểm A(1;-4) có 1 vectơ chỉ phương u = (-4;9)
2.
Đường thẳng d có 1 vtcp là \(\left(-2;3\right)\) hoặc \(\left(2;-3\right)\) cũng được
7.
Phương trình tham số của d: \(\left\{{}\begin{matrix}x=1-4t\\y=-4+9t\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2. VTCP: (-2;3)
7. \(d\left\{{}\begin{matrix}QuaA\left(1;-4\right)\\\overrightarrow{u}=\left(-4;9\right)\end{matrix}\right.\)=> PTTS \(\left\{{}\begin{matrix}x=1-4t\\y=-4+9t\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy,cho điểm A(-5;2) và đường thẳng d:\(\dfrac{x-2}{1}=\dfrac{y+3}{-2}\).Lập phương trình chính tắc của đường thẳng d' trong các trường hợp sau
a) d' đi qua A và song song với d
b)d' đi qua A và vuông góc với d
d nhận (1;-2) là 1 vtcp
a. d' song song d nên nhận (1;-2) là 1 vtcp
Phương trình d': \(\dfrac{x+5}{1}=\dfrac{y-2}{-2}\)
b. d' vuông góc d nên nhận \(\left(2;1\right)\) là 1 vtcp
Phương trình d': \(\dfrac{x+5}{2}=\dfrac{y-2}{1}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy,một đường thẳng đi qua điểm M(5;-3) cắt trục Ox và Oy tại A và B sao cho M là trung điểm của AB.Viết phương trình tổng quát của đường thẳng đó
Ta có: \(A\left(x_A;0\right)\) ; \(B\left(0;y_B\right)\Rightarrow\left\{{}\begin{matrix}\dfrac{x_A+0}{2}=5\\\dfrac{0+y_B}{2}=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(10;0\right)\\B\left(0;-6\right)\end{matrix}\right.\)
Phương trình d theo đoạn chắn:
\(\dfrac{x}{10}+\dfrac{y}{-6}=1\Leftrightarrow-3x+5y+30=0\)
Đúng 0
Bình luận (0)















