1B

2A

B

Đáp án A

+ Ta có: 

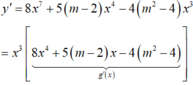
Ta xét các trường hợp sau

+  Nếu m²- 4= 0 hay m= ± 2

Khi m= 2 thì y’ = 8x⁷ nên x=0 là điểm cực tiểu.

Khi m=y’ = x⁴( 8x⁴- 20 ) khi đó x= 0 không là điểm cực tiểu.

+  Nếu m ≠  ± 2 .Khi đó ta có

Số cực trị của hàm y= x⁸+ (m-2) x⁵- ( m²- 4) x⁴+ 1  bằng số cực trị của hàm g’( x)

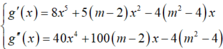
+Nếu x= 0 là điểm cực tiểu thì g’’ (0) >0.

Khi đó -4( m²- 4) > 0 hay -2< m< 2

Mà m nguyên nên m= -1; 0; 1

Kết hợp cả 3 trường hợp có 4 giá trị nguyên của m và tổng của chúng là:

2+ ( -1) +0+ 1=2

Chọn  D.

Chọn A

Xét hàm f x = 4 x x 4 + 1  trên  ℝ

Ta có  f ' x = 4 . 1 - 3 x 2 1 + 3 x 2 x 4 + 1 2

Từ đó  f ' x = 0

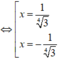
Ta có BBT

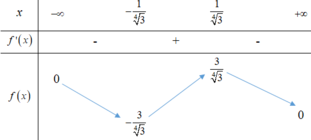
Từ BBT suy ra m ≥ 3 3 4 ≈ 2 , 27  mà m nguyên

và  m ∈ - 50 ; 50 ⇒ m ∈ 3 ; 4 ; . . . ; 50

Tổng  S = 3 + 4 + . . . + 50 = 1272

Ta có

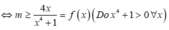
với ∀ x ∈ ℝ . ⇒ m ≥ m a x ℝ f ( x )

Xét hàm f ( x ) = 4 x x 4 + 1 trên ℝ  

Ta có

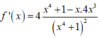
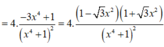
Từ đó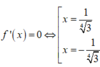 

Ta có BBT:

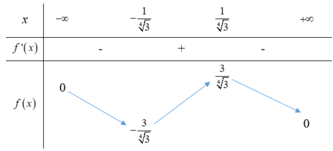
Từ BBT suy ra m ≥ 3 3 4 ≈ 2 , 27  mà m nguyên

và  m ∈ - 50 ; 50 ⇒ m ∈ 3 ; 4 ; . . ; 50

Tổng  S = 3 + 4 + . . + 50 = 3 + 50 . 48 2 = 1272

Chọn đáp án A.

\(h\left(x\right)=x^2-4x+5+m\)

\(g\left(x\right)=\left|h\left(x\right)\right|=\left|f\left(x\right)+m\right|=\left|x^2-4x+5+m\right|\)

\(h\left(0\right)=5+m;h\left(4\right)=5+m;h\left(2\right)=1+m\)

TH1: \(1+m>0\Leftrightarrow m>-1\)

\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)

TH2: \(5+m< 0\Leftrightarrow m< -5\)

\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)

TH3: \(5+m>0>1+m\Leftrightarrow-5< m< -1\)

Nếu \(5+m< -1-m\Leftrightarrow m< -3\)

\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)

Nếu \(5+m=-1-m\Leftrightarrow m=-3\)

\(max=5+m=2\ne9\)

\(\Rightarrow m=-3\) không thỏa mãn yêu cầu bài toán

Nếu \(5+m>-1-m\Leftrightarrow m>-3\)

\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)

Vậy \(m=4;m=-10\)