Phương trình của đường thẳng đi qua 2 điểm (0;2) và (2;0) là:
A. y= -x
B. y= -x+2
C. y= x+2
D. y= x-2
Những câu hỏi liên quan
cho 2 điểm P(4;0) , Q(0;-2) : a) viết phương trình tổng quát của đường thẳng đi qua điểm A(3;2) và song song với đường thẳng PQ ; b) viết phương trình tổng quát của đường trung trực của đoạn thẳng PQ .
cho 2 điểm P(4;0) , Q(0;-2) : a) viết phương trình tổng quát của đường thẳng đi qua điểm A(3;2) và song song với đường thẳng PQ ; b) viết phương trình tổng quát của đường trung trực của đoạn thẳng PQ .
\(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)
a) Đường thẳng qua A(3;2) song song với PQ nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\) làm VTCP nên có pt
\(\dfrac{x-3}{2}=\dfrac{y-2}{1}\Leftrightarrow x-2y+1=0\)
b) Đường thẳng trung trực của PQ qua trung điểm của PQ là M(2;-1) và nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)làm VTPT nên có pt
\(2(x-2)+(y+1)=0\Leftrightarrow 2x+y-3=0\)
Đúng 3
Bình luận (0)
cho 2 điểm P(4;0) , Q(0;-2) : a) viết phương trình tổng quát của đường thẳng đi qua điểm A(3;2) và song song với đường thẳng PQ ; b) viết phương trình tổng quát của đường trung trực của đoạn thẳng PQ .
Cho 3 điểm A ( 0; -8 ) , B ( 5/2 ; 2 ) , C ( 1; 7 ) và đường thẳng (d1) có phương trình 3x + 2y = -1
a, Viết phương trình đường thẳng (d2) đi qua hai điểm A và B
b, Viết phương trình đường thẳng (d3) đi qua điểm C và song song với (d1)
trong mặt phẳng xOy cho 2 điểm A<2,3>, B<1 ,-2> và đường thẳng d x-3y +1 bằng 0
a, viết phương trình tham số của đường thẳng P1 đi qua A và nhận u <1,-5> làm vecto chỉ phương
b, viết phương trình tổng quát của đường thẳng P2 đi qua B và vuông góc với đường thẳng d
c, tính khoảng cách từ gốc O đến đường thẳng AB
trong mặt phẳng xOy cho 2 điểm A<2,3>, B<1 ,-2> và đường thẳng d x-3y +1 bằng 0
a, viết phương trình tham số của đường thẳng Δ1 đi qua A và nhận u <1,-5> làm vecto chỉ phương
b, viết phương trình tổng quát của đường thẳng Δ2 đi qua B và vuông góc với đường thẳng d
c, tính khoảng cách từ gốc O đến đường thẳng AB
trong mặt phẳng xOy cho 2 điểm A<2,3>, B<1 ,-2> và đường thẳng d x-3y +1 bằng 0
a, viết phương trình tham số của đường thẳng P1 đi qua A và nhận u <1,-5> làm vecto chỉ phương
b, viết phương trình tổng quát của đường thẳng P2 đi qua B và vuông góc với đường thẳng d
c, tính khoảng cách từ gốc O đến đường thẳng AB
Viết phương trình tổng quát của đường thẳng đi qua điểm I (-1;2) và vuông góc với đường thẳng có phương trình 2x-y+4=0
Do d vuông góc 2x-y+4=0 nên d nhận (1;2) là 1 vtpt
Phương trình:
\(1\left(x+1\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-3=0\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y 0.a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với db) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng dc) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai
e
5
3
Đọc tiếp
Trong mặt phẳng tọa độ cho hai điểm A(3;0), B(0;2) và đường thẳng d: x + y = 0.
a) Lập phương trình tham số của đường thẳng Δ đi qua A và song song với d
b) Lập phương trình đường tròn đi qua A,B và có tâm thuộc đường thẳng d
c) Lập phương trình chính tắc của elip đi qua điểm B và có tâm sai e = 5 3
Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
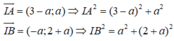
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
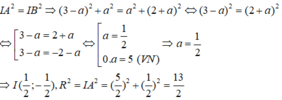
Vậy phương trình đường tròn có dạng:
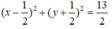
Ta có:
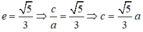
Giả sử elip (E) có dạng:
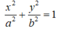
Vì (E) đi qua B nên:
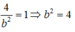
Mà
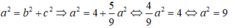
Vậy phương trình chính tắc của elip (E) là:
Đúng 0
Bình luận (0)
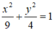
Viết phương trình đường thẳng \({d_1}\):
a) Đi qua điểm \(A(2;3)\) và song song với đường thẳng \({d_2}:x + 3y + 2 = 0\)
b) Đi qua điểm \(B(4; - 1)\) và vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\)
a) \({d_1}\) song song với đường thẳng \({d_2}:x + 3y + 2 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_2}\) làm vectơ pháp tuyến là \(\overrightarrow n = \left( {1;3} \right)\)
\({d_1}\) đi qua điểm \(A(2;3)\) nên ta có phương trình tổng quát
\(\left( {x - 2} \right) + 3.\left( {y - 3} \right) = 0 \Leftrightarrow x + 3y - 11 = 0\)
b) \({d_1}\) vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_3}\) làm vectơ chỉ phương là \(\overrightarrow u = \left( {3; - 1} \right)\)
\({d_1}\) đi qua điểm \(B(4; - 1)\) nên ta có phương trình tham số: \(\left\{ \begin{array}{l}x = 4 + 3t\\y = - 1 - t\end{array} \right.\)
Đúng 0
Bình luận (0)