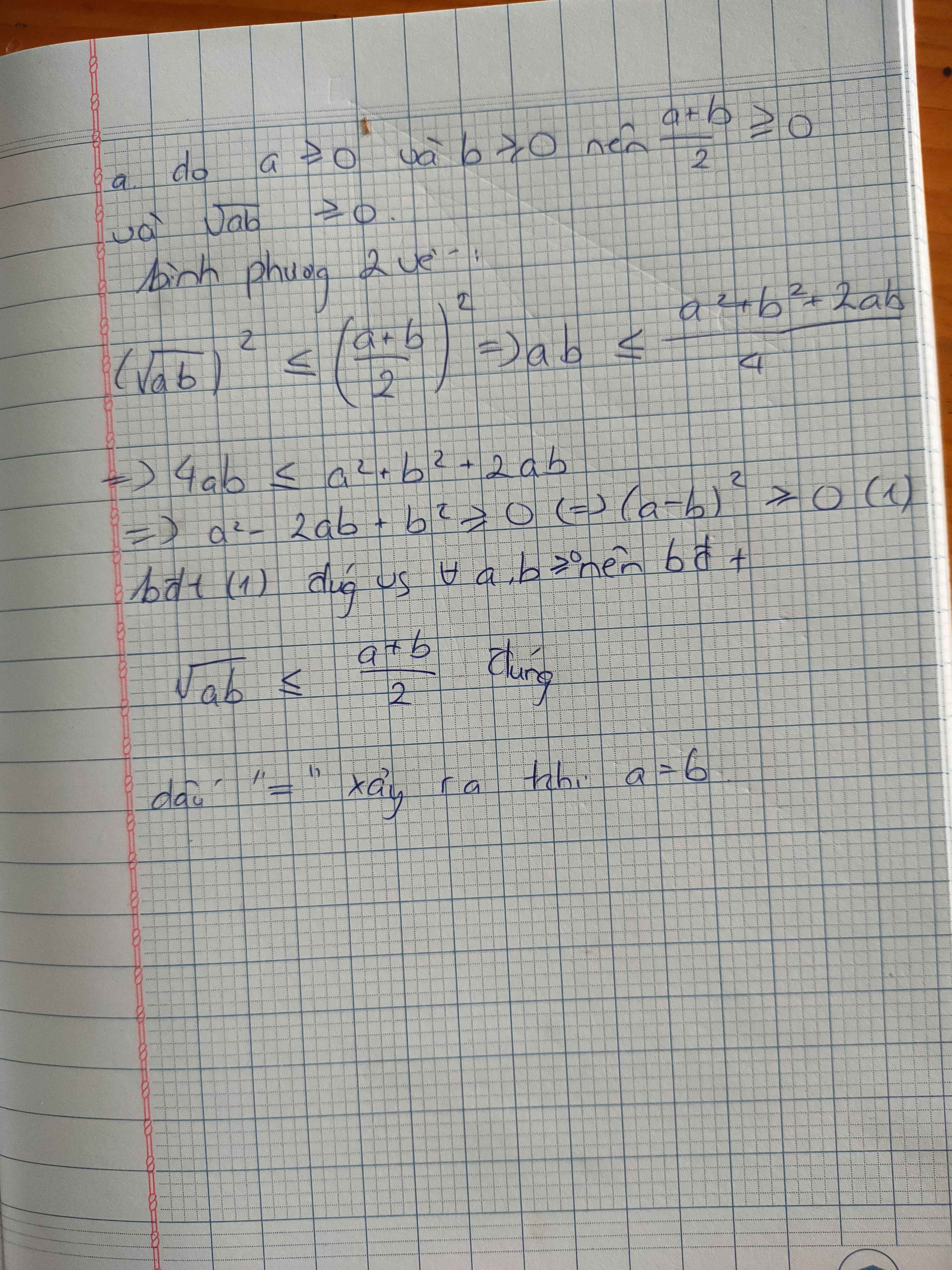cho A(0;1) và B(2b;-1). CMR đường trung trực của AB tiếp xúc với \(y=\frac{1}{4}x^2\)

Những câu hỏi liên quan
a) Cho m 2, chứng minh
m
2
−
2
m
0
.Cho a 0; b 0 và a b. Chứng minh
1
a
1
b
.Suy ra kết quả tương tự
a
≥
b
0
.
Đọc tiếp
a) Cho m > 2, chứng minh m 2 − 2 m > 0 .
Cho a < 0; b < 0 và a > b. Chứng minh 1 a < 1 b .
Suy ra kết quả tương tự a ≥ b > 0 .
a) Chú ý m > 2 thì m > 0.
b) Chú ý a < 0 và b < 0 thì ab > 0. Khi đó a > b, nhân hai vế với 1 ab > 0 ta thu được 1 b > 1 a . Tương tự a > 0, b > 0, a > b ta được 1 a < 1 b .
Đúng 0
Bình luận (0)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
Đúng 2
Bình luận (0)
Bài 1: Cho A= x(x-4). Với giá trị nào của x thì: A=0; A<0; A>0
Bài 2: Cho B= (x-3) : x (x khác 0). Với giá trị nào của x thì: B=0 ; B<0; B>0
a,cho T = 2013^0+2013^1+........+2013^2010.Tính 2012.T+1
b,cho a,n thuộc N khác 0 , a khác 0 ,a khác 1.Rút gọn tổng : a^0+a^1+a^2+.......+a^n
Chú ý: A²+B²=0 =>A=0,B=0
a) cho a²+b²+c²=ab+bc+ac. Cm a=b=c
b) cho a²-2a+b²+4b+4c²-4c+6=0. Tìm a,b,c?
a) We have :
a2 + b2 + c2 = ab + bc + ac
<=> 2a2 + 2b2 + 2c2 = 2ab + 2bc + 2ac
<=> 2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ac = 0
<=> (a2 - 2ab + b2) + (b2 - 2bc + c2) + (c2 - 2ac + a2) = 0
<=> (a - b)2 + (b - c)2 + (c - a)2 = 0
\(\Leftrightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}}\Rightarrow a=b=c\)
Đúng 0
Bình luận (0)
b) We have :
a2 - 2a + b2 + 4b + 4c2 - 4c + 6 = 0
(a2 - 2a + 1) + (b2 + 2.2b + 4) + (4c2 - 4c + 1) = 0
(a - 1)2 + (b + 2)2 + (2c - 1)2 = 0
\(\Leftrightarrow\hept{\begin{cases}a-1=0\\b+2=0\\2c-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=-2\\c=\frac{1}{2}\end{cases}}\)
Đúng 0
Bình luận (0)
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:

Đúng 0
Bình luận (0)
Cho A =x.(x-4/9) tìm x biết a) A= 0
b)A>0
c)A<0
a) \(A=x\left(x-\dfrac{4}{9}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{4}{9}\end{matrix}\right.\)
b) \(A=x\left(x-\dfrac{4}{9}\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x-\dfrac{4}{9}< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x-\dfrac{4}{9}>0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x< 0\\x>\dfrac{4}{9}\end{matrix}\right.\)
c) \(A=x\left(x-\dfrac{4}{9}\right)< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x-\dfrac{4}{9}< 0\end{matrix}\right.\)( do \(x>x-\dfrac{4}{9}\))
\(\Leftrightarrow\dfrac{4}{9}>x>0\)
Đúng 1
Bình luận (0)
a) A=x.(x-4/9)=0
<=>X=0 và X=4/9
b). A=x.(x-4/9)>0
<=>X>0 và X>4/9
c). A=x.(x-4/9)<0
<=>X<0 và X<4/9
Đúng 1
Bình luận (0)
b: Ta có: A<0
nên \(0< x< \dfrac{4}{9}\)
c: Ta có: A>0
nên \(\left[{}\begin{matrix}x< 0\\x>\dfrac{4}{9}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) Cho m > 0 và m < 1. Chứng minh m 2 < m
b) Cho a > b > 0. Chứng minh a 2 − b 2 > 0 .
a) Ta có M < 1. Mà m > 0 nên m.m < m.1 hay m 2 < m.
b) Từ a > b > 0, ta suy ra được a 2 > ab > b 2 . Sử dụng tính chất bắc cầu và liên hệ giữa thứ tự với phép cộng ta có a 2 - b 2 > 0.
Đúng 0
Bình luận (0)
Cho đa thức A(x)=ax2+bx+c
a) Chứng tỏ A(2).A(-1)<0 , biết 5a+b+2c=0
b) Cho A(x)=0 với mọi x . Chứng minh a=b=c=0
a)Mình nghĩ là chứng minh \(A\left(2\right).A\left(-1\right)\le0\)mới đúng chớ! Mình làm theo đề đã sửa nhé!
Ta có: \(A\left(2\right)=4a+2b+c\)
\(A\left(-1\right)=a-b+c\)
Suy ra \(A\left(2\right)+A\left(-1\right)=5a+b+2c=0\)
Suy ra \(A\left(2\right)=-A\left(-1\right)\)
Thay vào,ta có: \(A\left(2\right).A\left(-1\right)=-\left[A\left(-1\right)\right]^2\le0\) (đúng)
b)Theo đề bài A(x) = 0 với mọi x nên:
\(A\left(1\right)=a+b+c=0\Rightarrow a=-b-c\) (1)
\(A\left(-1\right)=a-b+c=0\Rightarrow b=a+c\) (2)
Cộng (1) và (2) lại,ta được: \(a+b=a-b\Leftrightarrow2b=0\Leftrightarrow b=0\) (*)
Khi đó \(A\left(x\right)=ax^2+c=0\forall x\)
\(\Rightarrow A\left(1\right)=a+c=0\Rightarrow a=-c\) (3)
\(A\left(2\right)=4a+c=0\Leftrightarrow-4a=c\) (4)
Cộng theo vế (3) và (4) suy ra \(-3a=0\Leftrightarrow a=0\) (**)
Thay a = b = 0 vào,ta có: \(A\left(x\right)=c=0\forall x\)(***)
Từ (*);(**) và (***) ta có a = b =c = 0 (đpcm)
Đúng ko ta?
Đúng 0
Bình luận (0)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy:
b) Cho a, b, c > 0. Chứng minh rằng:
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab.
ôi dào !dễ ợt ! cô em mới cho học ngày hôm qua !k đi rùi em trình bày cho cách làm !
Đúng 0
Bình luận (0)