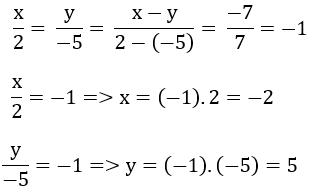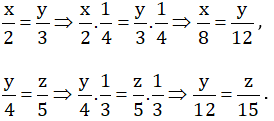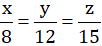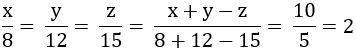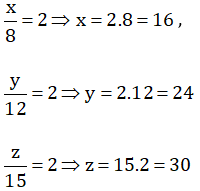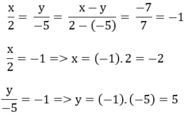a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{28}{7}=4\)

Do đó: x=12; y=16

\(a,Sửa:\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{28}{7}=4\\ \Rightarrow\left\{{}\begin{matrix}x=12\\y=16\end{matrix}\right.\\ b,\Rightarrow\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2+5}=\dfrac{-7}{7}=-1\\ \Rightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)

a/Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{28}{7}=4\)

=>x=4.3=12

=>y=4.4.=16

Vậy x=12 và y=16

b/Theo đề ta có:

\(\dfrac{x}{2}=\dfrac{y}{-5}\) và x-y=-7

Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:

\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)

=>x=-1.2=-2

=>y=-1.(-5)=5

Vậy x=-2 và y=5

cặc

Ta có: x/3 = y/4 => 4x = 3y

Mà x + y = 28 => 4(x + y) = 4.28 => 4x + 4y = 112   

Do đó 3y + 4y = 112

=> 7y = 112

=> y = 112/7 = 16

=> x = 28 - 16 = 12

b, Tương tự nha bạn

a) Áp dụng t/c dtsbn

\(\frac{x}{3}=\frac{y}{4}=\frac{x+y}{3+4}=\frac{28}{7}=4\)

\(\Rightarrow x=4.3=12\)

  \(y=4.4=16\)

b, Áp dụng t/c dtsbn

\(\frac{x}{2}=\frac{y}{-5}=\frac{x-y}{2-\left(-5\right)}=\frac{-7}{7}=-1\)

\(\Rightarrow x=-1.2=-2\)

  \(y=\left(-1\right).\left(-5\right)=5\)

Ta có : \(x=5x',y=5y'\)trong đó a' và b' là hai số nguyên tố cùng nhau

\(x+y=12\Rightarrow5\left(x'+y'\right)=12\Rightarrow x'+y'=12:5=2,4\)

Giả sử \(x'\ge y'\)thì x' = 2,3,y' = 1 hoặc x' = -2,6 , y = 5 => x = \(5\cdot2,3=11,5\)

Không thỏa mãn điều kiện vì 12 không chia hết cho 5

Ta có : \(x=8x',y=8y'\)(như trên)

Có \(x+y=32\Rightarrow8\left(x'+y'\right)=32\Rightarrow x'+y'=4\)

Giả sử \(x'\ge y'\)thì x' = 3 , y' = 1 hoặc x' = 1,y' = 3 => \(x=8\cdot3=24,y=8\cdot1=8\)hoặc \(x=8\cdot1=8,y=8\cdot3=24\)

Vậy \(\left(x,y\right)\in\left\{\left(24,8\right);\left(8,24\right)\right\}\)

á đù được của ló đấy

 \(\frac{x}{2}=\frac{y}{5}\)và x + y = -21
\(\frac{x}{2}=\frac{y}{5}=\frac{x+y}{2+5}=\frac{-21}{7}=-3\)
\(\Rightarrow\)\(\frac{x}{2}=-3\Rightarrow x=-3.2=-6\)
        \(\frac{y}{5}=-3\Rightarrow y=-3.5=-15\)
Bài 2 lập 1 đẳng thức trong 4 đẳng thức đã học rồi làm tương tự như trên nhé

1,                                                                                                                       2, 7x = 3y => x/3 = y/7   mà x - y = 16

ta có x/2 = y/5 mà x + y = -21                                                                             => 16/-4 = -4

=> -21/7 = -3                                                                                                            x = -4 x 3 = -12 ; y = -4 x 7 = -28

x = -3 x 2 = -6

y= -3 x 5 = -15

B1 : x/2 =y/5 và x+y = -21 

Áp dụng tính chất dãy tỷ số bằng nhau ta có : 

x/2 = y/ 5 = x+y/2+5 = -21/7 = -3 

=> x/2 = -3 

=> x = -6 

=> y/5 = -3

=. y = -15 

  thử lại xem đúng ko nha bn . 

a) Ta có: \(x:2=y:\left(-5\right)\)

nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)

mà x-y=-7

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)

Vậy: (x,y)=(-2;5)

b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)

nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)

Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)

nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)

Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)

mà x+y-z=10

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)

Vậy: (x,y,z)=(16;24;30)

b)

Do đó ta có 

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

x = -2

y = 5

Áp dụng t/c dtsbn ta có:

\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=-\dfrac{7}{7}=-1\)

\(\dfrac{x}{2}=-1\Rightarrow x=-2\\ \dfrac{y}{-5}=-1\Rightarrow y=5\)

Ta có

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{16}{8}=2\)

⇒ \(x=3.2=6\)

⇒ \(y=5.2=10\)

x/3 =y/5= x+y/3+5 = 16/8 =2

=> x/3 =2

     y/5 =2

=> x= 6

     y=10

\(\dfrac{x}{3}=\dfrac{y}{5}\Rightarrow5x=3y\Rightarrow x=\dfrac{3}{5}y\)

Thay vào, ta có:

\(x+y=16\Rightarrow y+\dfrac{3}{5}y=16\)

\(\dfrac{8}{5}y=16\Rightarrow y=10\\ \Rightarrow x=6\)

Áp dụng tc dtsbn:

\(\dfrac{x}{y}=\dfrac{5}{3}\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x+y}{5+3}=\dfrac{64}{8}=8\\ \Leftrightarrow\left\{{}\begin{matrix}x=40\\y=24\end{matrix}\right.\)