Tìm m để phương trình \(x^2-4x+m+2=0\) có 2 nghiệm x1; x2 thỏa mãn \(\left(x_1\right)^3+\left(x_2\right)^3=28\)

Những câu hỏi liên quan
Cho phương trình: \(x^2-4x+2m=0\) (x là ấn phụ)
a) Tìm m để phương trình có 2 nghiệm x1 và x2
b) Gọi x1 và x2 là 2 nghiệm của phương trình trên. Tìm m để \(x1^2+x2^2-x1-x2=16\)
a.
Phương trình có 2 nghiệm khi:
\(\Delta'=4-2m\ge0\Rightarrow m\le2\)
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=2m\end{matrix}\right.\)
\(x_1^2+x_2^2-x_1-x_2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=16\)
\(\Leftrightarrow16-4m-4=16\)
\(\Leftrightarrow m=-1\) (thỏa mãn)
Đúng 2
Bình luận (0)
a.\(\Delta=\left(-4\right)^2-4.2m=16-8m\)
Để pt có nghiệm x1, x2 thì \(\Delta>0\)
\(\Leftrightarrow16-8m>0\)
\(\Leftrightarrow-8m>-16\)
\(\Leftrightarrow m< 2\)
b.
Theo hệ thức Vi-ét, ta có:\(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=2m\end{matrix}\right.\)
\(x_1^2+x_2^2-x_1-x_2=16\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2-\left(x_1+x_2\right)=16\)
\(\Leftrightarrow4^2-2.2m-4-16=0\)
\(\Leftrightarrow-4m-4=0\)
\(\Leftrightarrow m=-1\)
Đúng 1
Bình luận (0)
Cho phương trình (ấn số x): x 2 – 4x + m – 2 = 0 (1)
b) Tìm m để phương trình (1) có 2 nghiệm x 1 , x 2 thỏa mãn 3 x 1 – x 2 = 8
b) Theo hệ thức Vi-et ta có:
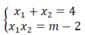
Theo bài ra:
3 x 1 - x 2 = 8
⇔ 3 x 1 - x 2 = 2( x 1 + x 2 )
⇔ x 1 = 3 x 2
Khi đó: x 1 + x 2 = 4 ⇔ 3 x 2 + x 2 = 4 ⇔ 4 x 2 = 4 ⇔ x 2 = 1
⇒ x 1 = 3
⇒ x 1 x 2 = 3 ⇒ m - 2 = 3 ⇔ m = 5
Vậy với m = 5 thì phương trình có 2 nghiệm thỏa mãn yêu cầu đề bài.
Đúng 1
Bình luận (0)
Cho phương trình x^2 -4x+m-5=0 tìm các giá trị m để phương trình có 2 nghiệm phân biệt x1,x2 thoã mãn(x1-1).(x2^2-3x2+m-6)=-3
=>(x1-1)[x2^2-x2(x1+x2-1)+x1x2+1]=-3
=>(x1-1)[-x1x2+x2+x1x2+1]=-3
=>(x1-1)(x2+1)=-3
=>x1x2+(x1-x2)-1=-3
=>(x1-x2)=-3+1-x1x2=-2-m+5=-m+3
=>(x1+x2)^2-4x1x2=m^2-6m+9
=>4^2-4(m-5)=m^2-6m+9
=>4m-20=16-m^2+6m-9=-m^2+6m+7
=>4m-20+m^2-6m-7=0
=>m^2-2m-27=0
=>\(m=1\pm2\sqrt{7}\)
Đúng 0
Bình luận (0)
Bài 5: Cho phương trình x2 – 4x + 2m - 3 = 0 a) Tìm điều kiện của m để phương trình có 2 nghiệm x1, X2 phân biệt thoả tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau. b) Tìm m để phương trình có 2 nghiệm X), x2 thoả mãn điều kiện x1 = 3x2
a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)
Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2
nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì
\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau
Đúng 1
Bình luận (0)
Cho phương trình bậc hai ( ẩn x) : x² + 4x + m +1= 0 (*) (m là tham số)
a) Giải phương trình khi m = -1
b) Tìm m để phương trình có một nghiệm bằng 2.Tìm nghiệm còn lại.
c) Tìm m để phương trình có hai nghiệm x1,x2 thỏa mãn x12 + x12 =10.
a)thay m=1 vào pt ta có
\(x^2+4x=0\)
<=> \(\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b) thay x=2 vào pt ta có: 13+m=0
<=>m=-13
thay m=-13 vào pt ta có
\(x^2+4x-12=0\)
<=>(x-2)(x+6)=0
<=>\(\left[{}\begin{matrix}x=2\\x=-6\end{matrix}\right.\)\(\)
vậy với m=-13 thì nghiệm còn lại là x=-6
c) để pt có 2 nghiệm pb thì \(\Delta>0\)
<=>16-4m-4>0
<=>3-m>0
<=>m<3
áp dụng định lí Vi-ét ta có\(\left\{{}\begin{matrix}x_1+x_2=-4\\x_1x_2=m+1\end{matrix}\right.\)
theo đề bài ta có \(x_1^2+x_2^2=10\)
<=>\(\left(x_1+x_2\right)^2-2x_1x_2=10\)
<=>16-2m-2=10
<=>2-m=0
<=>m=2(nhận)
vậy với m=2 thì pt có 2 nghiệm pb thỏa yêu cầu đề bài.
Đúng 1
Bình luận (0)
cho phương trình x^2-4x+m+1=0 tìm m để pt (2) có 2 nghiệm x1*x2 thỏa mãn x1^2+x2^2=12
\(pt:x^2-4x+m+1=0\)
\(\Delta=b^2-4ac=\left(-4\right)^2-4.1.\left(m+1\right)\)\(=16-4m-4=12-4m\)
Phương trình có hai nghiệm x1 ,x2 :
\(\Leftrightarrow\Delta\ge0\Leftrightarrow12-4m\ge0\Leftrightarrow m\le3\)(1)
Theo hệ thức Viet ta có :
\(\hept{\begin{cases}x_1+x_2=4\\x_1.x_2=m+1\end{cases}}\)
\(x_1^2+x_2^2=12\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=12\)
\(\Leftrightarrow16-2m-2=12\Leftrightarrow14-2m=12\Leftrightarrow2m=2\Leftrightarrow m=1\)( TMĐK (1))
Vậy m = 1
Đúng 1
Bình luận (0)
Cho pt xã -4x4 m=0 (*). Tìm m để phương trình (*) có 2 nghiệm x1, x2 thỏa mãn hệ thức 2x1 + x2 = 1 Cho pt: 2x2 3x-2m +3 = 0 ("). Tìm m để phương trình (") có 2 nghiệm phân biệt x1, x2 thỏa mãn hệ thức x1/x2 + xz/x1 =3 Cho pt xã 4x - m + 3 = 0 (*). Tìm m để phương trình (*) có 2 nghiệm x1, x2 thỏa mãn hệ thức x1-x2=7 Giải gấp chi tiết giúp e vs ạ
X^2-2(m-1)x-2m=0 a, Tìm m để phương trình có 2 nghiệm phân biệt t/m x1^2+x1-x2=5-2m b,Tìm m để p trình có 2 nghiệm pb t/m x1=3x2 c,Tìm m để phương trình có 2 no pb t/m x1/x2=3
b: x1=3x2 và x1+x2=2m-2
=>3x2+x2=2m-2 và x1=3x2
=>x2=0,5m-0,5 và x1=1,5m-1,5
x1*x2=-2m
=>-2m=(0,5m-0,5)(1,5m-1,5)
=>-2m=0,75(m^2-2m+1)
=>0,75m^2-1,5m+0,75+2m=0
=>\(m\in\varnothing\)
c: x1/x2=3
x1+x2=2m-2
=>x1=3x2 và x1+x2=2m-2
Cái này tương tự câu b nên kết quả vẫn là ko có m thỏa mãn
Đúng 0
Bình luận (0)
Cho phương trình: x^2 + 4x + m + 1 = 0. Tìm m để pt có 2 nghiệm x1, x2 thỏa mãn pt \(\dfrac{x1}{x2}+\dfrac{x2}{x1}=\dfrac{10}{3}\)
PT có 2 nghiệm `<=> \Delta' >0 <=> 2^2-1.(m+1)>0<=> m<3`
Viet: `x_1+x_2=-4`
`x_1 x_2=m+1`
`(x_1)/(x_2)+(x_2)/(x_1)=10/3`
`<=> (x_1^2+x_2^2)/(x_1x_2)=10/3`
`<=> ((x_1+x_2)^2-2x_1x_2)/(x_1x_2)=10/3`
`<=> (4^2-2(m+1))/(m+1)=10/3`
`<=> m=2` (TM)
Vậy `m=2`.
Đúng 1
Bình luận (0)
cho pt \(x^2-4x+m^2-3m=0\) Tìm m để phương trình có hai nghiệm x1,x2 thỏa mãn \(x_1=x_2^2-4x_2\)























