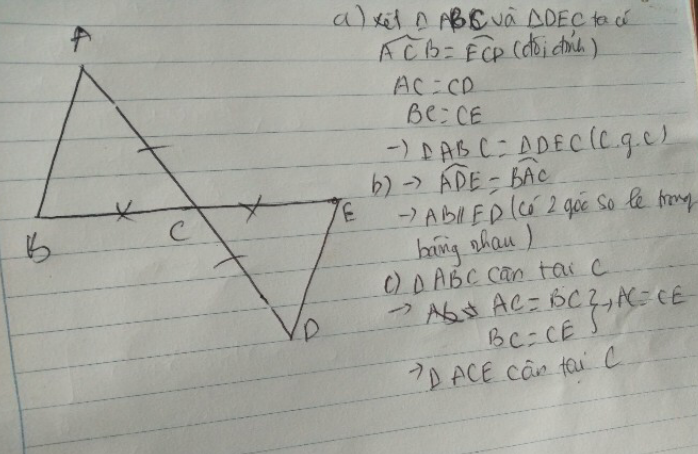Cho ΔABC; vẽ các tia phân giác của\(\widehat{B}\)và\(\widehat{C}\) cắt cạnh AC và AB tại D và E, biết \(\widehat{ADB}\)=\(\widehat{BEC}\).Tính số đo của \(\widehat{A}\).

Những câu hỏi liên quan
a)Cho ΔABC có a=5,b=6,góc ACB=30 độ.Tính cạnh AB
b)Cho ΔABC cân tại A,có cạnh AB=a.Tính số đo các cạnh,các góc còn lại của ΔABC và tính bán kính đường tròn ngoại tiếp ΔABC biết góc A=70 độ
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP√30cm,NP√14 cmBài2:Cho ΔABC cân tại A. Biết AB2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH6cm,HB4cm,HC9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH4cm,HB2cm,HC8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB4cm,HB2cm,HC8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB6cm,AC8cm và dfrac{HB}{HC}dfrac{9}{16}Tính HB,HC
Đọc tiếp
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC. Lấy điểm D, E sao cho C là trung điểm của BE và AD. Chứng minh:
a) ΔABC = ΔDEC; b) AB // DE
c) Nếu ΔABC cân tại C thì ΔAEC là tam giác gì? Vì sao?
Cho ΔABC có AB=2; BC=3;AC=6 a) Tính diện tích ΔABC=? b) Tính độ dài đường trung tuyến kẻ từ C c) Tính bán kính đường tròn ngoại tiếp ΔABC d) Tính số đo góc lớn nhất trong ΔABC.
AB+BC<AC
nên ko có tam giác ABC thỏa mãn nha bạn
Đúng 2
Bình luận (0)
Cho ΔABC vuông tại B biết: BC=2a; góc A=45°: a) Tính độ dài cạnh AB; AC b) Kẻ BH vuông góc AC. Tính BH=? c) Tính diện tích ΔABC d) Tính chu vi ΔABC e) Tính bán kính đường tròn ngoại tiếp ΔABC
a: ΔBAC vuông tại B có góc A=45 độ
nên ΔBAC vuông cân tại B
=>BA=BC=2a
AC=căn AB^2+BC^2=2a*căn 2
b: BH=BA*BC/AC=4a^2/2*a*căn 2=a*căn 2
c: S ABC=1/2*2a*2a=2a^2
d: C=2a+2a+2a*căn 2=4a+2a*căn 2
Đúng 0
Bình luận (0)
Cho ΔABC vuông cân tại A , có cạnh BC =3a . Hảy tính diện tích ΔABC.
\(AB=\sqrt{\dfrac{BC^2}{2}}=\sqrt{\dfrac{9a^2}{2}}=\sqrt{\dfrac{18a^2}{4}}=\dfrac{3a\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{18a^2}{4}:2=\dfrac{18a^2}{8}=\dfrac{9a^2}{4}\)
Đúng 1
Bình luận (0)
Cho ΔABC: góc A = 90o, AH⊥BC. Tính diện tích ΔABC. Biết AH = 12cm, BH= 9cm
BC=9cm chứ?
`S_{DeltaABC}=(AH.BC)/2=(12.9)/2=6.9=54cm^2`
Đúng 0
Bình luận (0)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow CH=\dfrac{12^2}{9}=\dfrac{144}{9}=16\left(cm\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot25}{2}=\dfrac{300}{2}=150\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC đều cạnh 3a. Hảy tính độ dài đường cao BH và diện tích ΔABC.
BH là đường cao nên cũng là đường trung trực của tam giác ABC đều
\(\Rightarrow BH\perp AC\) tại H cũng là trung điểm của BC
\(\Rightarrow AH=HC=\dfrac{1}{2}AC=\dfrac{3}{2}a\)
Vì \(\Delta AHB\) vuông tại H nên \(BH=\sqrt{AB^2-AH^2}=\sqrt{9a^2-\dfrac{9}{4}a^2}=\dfrac{3a\sqrt{3}}{2}\)
\(S_{ABC}=\dfrac{1}{2}BH\cdot AC=\dfrac{1}{2}\cdot\dfrac{3a\sqrt{3}}{2}\cdot3a=\dfrac{9a^2\sqrt{3}}{4}\left(đvdt\right)\)
Đúng 1
Bình luận (0)
Cho ΔABC vuông cân ở A , đường cao AH = 2cm
a) C/m ΔABC∼ΔHCA
b) Tính AB , HC
a) Xét ΔABC vuông tại A và ΔHCA vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHCA(g-g)
b) Ta có: ΔABC\(\sim\)ΔHCA(cmt)
nên \(\dfrac{AB}{HC}=\dfrac{AC}{AH}=\dfrac{BC}{CA}\)
\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{HC}{AH}=1\)
\(\Leftrightarrow HC=AH=2\left(cm\right)\)
Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC vuông cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(hai cạnh tương ứng)
mà HC=2cm(cmt)
nên HB=2cm
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=8\)
hay \(AB=2\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔDHE ~ ΔABC với tỉ số đồng dạng
2
3
. Có bao nhiêu khẳng định đúng trong các khẳng định sau:(I) Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là
2
3
.(II) Tỉ số hai đường cao tương ứng của ΔABC và ΔDHE là
2
3
.(III) Tỉ số diện tích của ΔABC và ΔDHE là
2
3
.(IV) Tỉ số diện tích của ΔDHE và ΔABC là
4
9...
Đọc tiếp
Cho ΔDHE ~ ΔABC với tỉ số đồng dạng 2 3 . Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là 2 3 .
(II) Tỉ số hai đường cao tương ứng của ΔABC và ΔDHE là 2 3 .
(III) Tỉ số diện tích của ΔABC và ΔDHE là 2 3 .
(IV) Tỉ số diện tích của ΔDHE và ΔABC là 4 9
A. 2
B. 1
C. 3
D. 4
Vì ΔDHE ~ ΔABC với tỉ số đồng dạng 2 3 nên tỉ số hai đường cao tương ứng của ΔDHE và ΔABC là 2 3 và tỉ số diện tích của ΔDHE và ΔABC là ( 2 3 ) 2 = 4 9
Do đó (I) và (IV) đúng, (II) và (III) sai.
Đáp án: A
Đúng 0
Bình luận (0)