Cho hai số m; n nguyên dương và nguyên tố cùng nhau thỏa mãn m + n = 90. Tìm giá trị lớn nhất của m.n
MÌNH ĐANG CẦN RẤT GẤP
Cho hai hàm số y = m + 1 x 2 + 3 m 2 x + m và y = m + 1 x 2 + 12 x + 2 . Tìm tất cả các giá trị của tham số m để đồ thị hai hàm số đã cho không cắt nhau.
A. m = 2.
B. m = −2.
C. m = ±2.
D. m = 1.
Đồ thị hai hàm số không cắt nhau khi và chỉ khi phương trình
m + 1 x 2 + 3 m 2 x + m = m + 1 x 2 + 12 x + 2 vô nghiệm
⇔ 3 m 2 - 4 x = 2 - m vô nghiệm
⇔ m 2 − 4 = 0 2 − m ≠ 0 ⇔ m = ± 2 m ≠ 2 ⇔ m = − 2
Đáp án cần chọn là: B
Cho hai số có hai chữ số mà số lớn bằng 3 lần số bé. Nếu đem số bé viết thêm vào bên phải và bên trái số lớn ta được hai số mới mỗi số có 4 chữ số. Tổng của hai số có 4 chữ số đó bằng 4848. Tìm hai số đã cho.
Ta có: \(\overline{ab}\)\(=\overline{cd}\)\(.3\)
\(\overline{abcd}\)\(+\)\(\overline{cdab}\)\(=4848\)\(\Rightarrow\overline{ab}\)\(+\overline{cd}\)\(=48\)
Ta giải theo tổng tỉ.
Số bé là: \(48:\left(3+1\right).1=12\)
Số lớn là: \(12.3=36\).
Cho hai hàm số: y = (3m + 1)x – 5 và y = − 2x + 1. Giá trị nào của m để đồ thị hai hàm số đã cho là hai đường thẳng song song với nhau?
A m= 1
B m= -5
C m= -2
Dm= -1
cho hai hàm số bậc nhất là y=(1+m)x-m và y=2021x-2. Tìm các giá trị của tham số m để đồ thị hai hàm số đã cho song song với nhau.
Để hai đường thẳng song song thì m+1=2021
hay m=2020
Cho phương trình (m+2)x2−2(m−1)x+3−m=0 (1); với m là tham số thực
1) Giải và biện luận phương trình đã cho theo tham số m
2) Tìm m để phương (1) có hai nghiệm thỏa mãn tổng hai nghiệm bằng tích hai nghiệm.
1: Ta có: \(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\cdot\left(m+2\right)\left(3-m\right)\)
\(=\left(2m-2\right)^2+4\left(m+2\right)\left(m-3\right)\)
\(=4m^2-8m+4+4\left(m^2-3m+2m-6\right)\)
\(=4m^2-8m+4+4m^2-4m-24\)
\(=-12m-20\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow-12m-20>0\)
\(\Leftrightarrow-12m>20\)
hay \(m< \dfrac{-5}{3}\)
Để phương trình có nghiệm kép thì Δ=0
\(\Leftrightarrow-12m-20=0\)
\(\Leftrightarrow-12m=20\)
hay \(m=\dfrac{-5}{3}\)
Để phương trình vô nghiệm thì Δ<0
\(\Leftrightarrow-12m-20< 0\)
\(\Leftrightarrow-12m< 20\)
hay \(m>\dfrac{-5}{3}\)
2: ĐKXĐ: \(m\ne-2\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+2}=\dfrac{2m-2}{m+2}\\x_1\cdot x_2=\dfrac{3-m}{m+2}\end{matrix}\right.\)
Ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow\dfrac{2m-2}{m+2}=\dfrac{3-m}{m+2}\)
Suy ra: 2m-2=3-m
\(\Leftrightarrow2m+m=3+2\)
\(\Leftrightarrow3m=5\)
hay \(m=\dfrac{5}{3}\)(thỏa ĐK)
cho hai số tự nhiên m và n , m là số tự nhiên lẻ.Chứng tỏ m và mn+8 là hai số nguyên tố cùng nhau
Gọi a=ƯC(m,mn+8)
Ta có : m chia hết cho a (m lẻ suy ra a lẻ)
suy ra mn chia hết cho a
Lại có :mn+8 chia hết cho a
suy ra :mn+8 chia hết cho a
suy ra a\(\in\) Ư(8)=(1,2,4,8)
vì a lẻ
\(\Rightarrow\)a=1
\(\Rightarrow\)ƯC(m,mn+8)=1
\(\Rightarrow\)m và mn+8 là 2 số nguyên tố cùng nhau
Cho hai hàm sốbậc nhất y=m2 x+m-1 và y=4x+3-m trong đó m là tham số. Tìm tất cả các giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song với nhau?
Đề hai đường thẳng song song thì \(\left\{{}\begin{matrix}m^2=4\\m-1\ne3-m\end{matrix}\right.\Leftrightarrow m=-2\)
Để 2 đt song song thì
\(\left\{{}\begin{matrix}m^2=4\\m-1\ne3-m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\ne2\end{matrix}\right.\Leftrightarrow m=-2\)
1 .Tìm hai phân số có tử số là Mẫu số là số tự nhiên liên tiếp sao cho 2/13 nằm giữa hai phân số đó
2 . Tìm hai số có mẫu số là 7 tử số là hai số tự nhiên liên tiếp sao cho 3/4 nằm giũa hai phân số đó
3 . Tìm hai số biết hiệu là 82 nếu thêm 1 số vào bên phải một số nào đó thì được số lớn . Ai làm đúng mình tích cho . ( Mình ko biết tích . Chỉ mình với nhé . Xí hổ )
Mình cần gấp lắm . 3 ko phải chương phan so
Cho hai hàm số y = 3x + k và y = (m -2)x + (2k + 3). Biết rằng đồ thị hai hàm số đã cho trùng nhau. Tính m + k ?
A. 1
B. -2
C.3
D. 2
Đáp án D
Vì đồ thị hai hàm số đã cho trùng nhau nên:
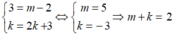
Cho hai hàm số bậc nhất y = (m + 1)x + 2m và y = (2m + 1)x + 3m. 1) Tìm giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song. 2) Tìm giá trị của m để giao điểm của hai đồ thị đã cho nằm trên trục hoành.
1. Để 2 đồ thị hàm số đã cho là hai đường thẳng song song thì
\(\left\{{}\begin{matrix}m+1=2m+1\\2m\ne3m\end{matrix}\right.\left(ĐK:m\ne-1,-\dfrac{1}{2}\right)\)
Hệ phương trình tương đương với:
\(\left\{{}\begin{matrix}m=0\\m\ne0\end{matrix}\right.\Rightarrow\text{Hệ\:phương\:trình\:vô\:nghiệm}\)
Vậy không tồn tại giả trị m để đồ thị của hai hàm số trên song song.
2. Để giao điểm hai đồ thì nằm trên trục hoành thì y = 0.
\(y=\left(m+1\right)x+2m=0\Rightarrow x=-\dfrac{2m}{m+1}\) (1)
\(y=\left(2m+1\right)x+3m=0\Rightarrow x=-\dfrac{3m}{2m+1}\) (2)
và \(m+1\ne2m+1\Rightarrow m\ne0\) (3)
Từ (1) và (2) và (3) ta tìm được m = 1.