Hình chóp SABC có SA vuông góc với mặt phẳng (ABC); tam giác ABC đều cạnh 2a; góc giữa (SBC) và (ABC) bằng 45 ° . Tính khoảng cách h từ A tới mặt phẳng (SBC).
A. h = a 2 3
B. h = a 3 2
C. h = a 3 4
D. h = a 2
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Thể tích của khối chóp SABC bằng
A. a 3 3 8
B. a 3 12
C. a 3 3 4
D. a 3 3 12
Cho hình chóp SABC có đáy là tam giác đều cạnh α , SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 600. Thể tích của khối chóp SABC bằng
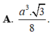
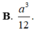
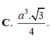
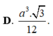
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 0 . Tính thể tích V của khối chóp SABC.
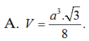
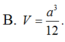

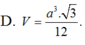
Cho hình chóp SABC có đáy là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy, góc giữa hai mặt phẳng (SBC) và (ABC) bằng 60 ° . Tính thể tích V của khối chóp SABC
A. V = a 3 3 8
B. V = a 3 12
C. V = a 3 3 4
D. V = a 3 3 12
Cho hình chóp SABC có SA vuông góc với ABC và AB vuông góc với BC.Góc giữa hai mặt phẳng SBC và ABC là góc nào
\(\left\{{}\begin{matrix}SA\perp BC\\AB\perp BC\end{matrix}\right.\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\left\{{}\begin{matrix}BC\perp SB\\BC\perp AB\\\left(SAB\right)\cap\left(SBC\right)=BC\end{matrix}\right.\Rightarrow\left(\left(SAB\right),\left(SBC\right)\right)=\left(SB,AB\right)=\widehat{SBA}\)
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), hai mặt phẳng (SAB) và (SBC) vuông góc với nhau, S B = a 3 , B S C ^ = 45 ° , A S B ^ = 30 ° Thể tích khối chóp SABC là V. Tỉ số a 3 V là
A . 8 3
B . 8 3 3
C . 2 3 3
D . 4 3
Cho hình chóp sabc có SA vuông góc với mặt phẳng (abc) là tam giác vuông tại B, bc=2a. Khoảng cách từ C đến mặt phẳng (sab) bằng
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=2a\)
Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B , SA vuông góc với ABC ,SA = a√3 . Xác định và tính góc giữa hai mặt phẳng SBC và ABC
\(SB=\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\)
\(SC=\sqrt{SA^2+AC^2}=a\sqrt{5}\)
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
(SBC;ABC)=(SB;BA)=góc SBA=60 độ
Cho hình chóp SABC có ABC=60 độ,AC=\(a\sqrt{3}\).Cạnh bên SA vuông góc với mặt phẳng đáy,SA=2a.Thể tích của khối cầu ngoại tiếp hình chóp S.ABC
Lời giải:
Gọi $I$ là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$, $K$ là tâm đường tròn ngoại tiếp $ABC$ thì $IK\parallel SA$.
Ta có:
\(IS=IA\Leftrightarrow (\overrightarrow{IS})^2=IA^2\)
\(\Leftrightarrow (\overrightarrow{IA}+\overrightarrow{AS})^2=IA^2\)
\(\Leftrightarrow AS^2+2\overrightarrow{IA}.\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2(\overrightarrow{IK}+\overrightarrow{KA})\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2\overrightarrow{IK}.\overrightarrow{AS}=0\)
Vì $\overrightarrow{IK}\parallel \overrightarrow{AS}$ nên tồn tại $k\in\mathbb{R}$ sao cho $\overrightarrow{IK}=k\overrightarrow{AS}$
Khi đó: $AS^2+2kAS^2=0$
$\Rightarrow k=-\frac{1}{2}$
$\Rightarrow \overrightarrow{IK}=\frac{-1}{2}\overrightarrow{AS}$
$\Rightarrow IK=\frac{1}{2}.AS=a$
Lại có:
$\frac{AC}{\sin B}=2AK\Rightarrow AK=a$
Áp dụng định lý pitago: $R=IA=\sqrt{IK^2+AK^2}=\sqrt{2}a$
Thể tích khối cầu:
$V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi a^3$