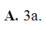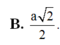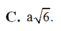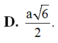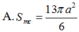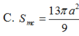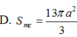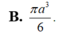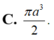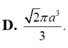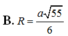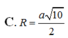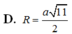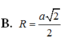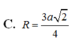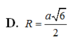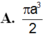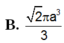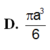Lời giải:
Gọi $I$ là tâm mặt cầu ngoại tiếp hình chóp $S.ABC$, $K$ là tâm đường tròn ngoại tiếp $ABC$ thì $IK\parallel SA$.
Ta có:
\(IS=IA\Leftrightarrow (\overrightarrow{IS})^2=IA^2\)
\(\Leftrightarrow (\overrightarrow{IA}+\overrightarrow{AS})^2=IA^2\)
\(\Leftrightarrow AS^2+2\overrightarrow{IA}.\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2(\overrightarrow{IK}+\overrightarrow{KA})\overrightarrow{AS}=0\)
\(\Leftrightarrow AS^2+2\overrightarrow{IK}.\overrightarrow{AS}=0\)
Vì $\overrightarrow{IK}\parallel \overrightarrow{AS}$ nên tồn tại $k\in\mathbb{R}$ sao cho $\overrightarrow{IK}=k\overrightarrow{AS}$
Khi đó: $AS^2+2kAS^2=0$
$\Rightarrow k=-\frac{1}{2}$
$\Rightarrow \overrightarrow{IK}=\frac{-1}{2}\overrightarrow{AS}$
$\Rightarrow IK=\frac{1}{2}.AS=a$
Lại có:
$\frac{AC}{\sin B}=2AK\Rightarrow AK=a$
Áp dụng định lý pitago: $R=IA=\sqrt{IK^2+AK^2}=\sqrt{2}a$
Thể tích khối cầu:
$V=\frac{4}{3}\pi R^3=\frac{8\sqrt{2}}{3}\pi a^3$