Tam giác ABC vuông tại A \(\Rightarrow\) góc B + góc C = 90 độ

Tam giác AHB vuông tại H \(\Rightarrow\) góc B + góc BAH = 90 độ

Suy ra góc C = góc BAH (cùng phụ góc B)

a) Xét \(\Delta ABH\)có:

\(\widehat{BAH}+\widehat{ABH}+\widehat{AHB}=180^o\)( đl tổng 3 góc của 1 tam giác)

hay \(\widehat{BAH}+60^o+90^o=180^o\)

\(\Rightarrow\widehat{BAH}=30^o\)

b) Xét \(\Delta ABC\)và \(\Delta CDA\)có:

\(AB=CD\left(gt\right)\)

\(\widehat{BAC}=\widehat{ACD}\)( 2 góc slt)

\(AC\)cạnh chung

\(\Rightarrow\Delta ABC=\Delta CDA\left(c-g-c\right)\)

\(\Rightarrow\widehat{ACB}=\widehat{CAD}\)( 2 góc tương ứng)

c) Ta có: \(\widehat{ACB}=\widehat{CAD}\)( c/mt)

Mà 2 góc này nằm ở vị trí slt

\(\Rightarrow AD//BC\)

\(\Rightarrow\widehat{AHB}=\widehat{HAD}\)(2 góc slt)

Mà \(\widehat{AHB}=90^o\left(gt\right)\)

\(\Rightarrow\widehat{HAD}=90^o\)

Hay nói cách AD vuông góc AH( đpcm)

học tốt!!

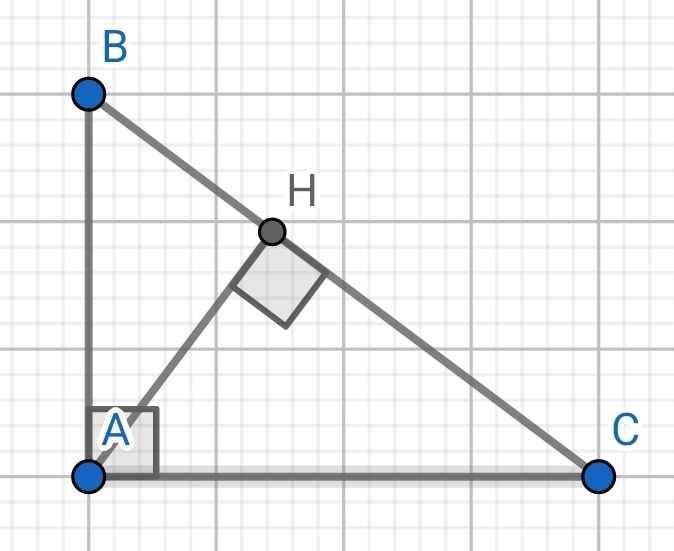
∆AHB vuông tại H

⇒∠BAH + ∠ABH = ∠BAH + ∠ABC = 90⁰ (1)

∆ABC vuông tại A

⇒ ∠ABC + ∠ACB = 90⁰ (2)

Từ (1) và (2) ⇒ ∠BAH = ∠ACB

Hay ∠BAH = ∠C

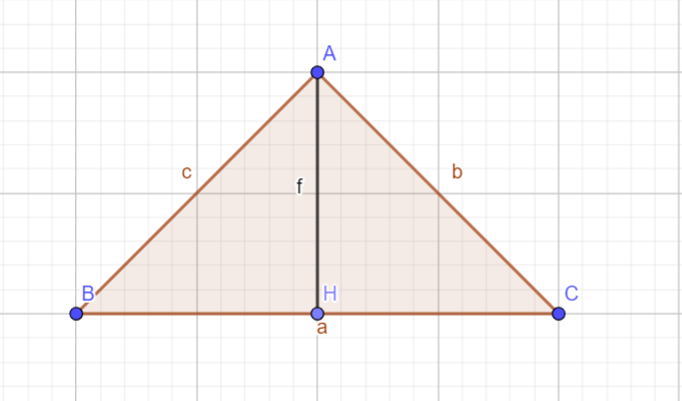
a) Xét tam giác AHB và AHC có:

AC = BC (gt)

\(\widehat{AHB}=\widehat{AHC}\) (AH vuông góc BC)

=> AHB = AHC (ch-gv)

=> HB = HC (cạnh tương ứng)

\(\widehat{BAH}=\widehat{CAH}\) (góc tương ứng)

b) Ta có HB =  HC (cmt)

Mặt khác AH là cạnh góc vuông của tam giác vuông AHC

Áp dụng định lý Pitago ta có:

\(AC^2=AH^2+HC^2\\ =>10^2=AH^2+6^2\\ =>100=AH^2+36\)

\(=>AH^2=100-36=64\\ =>AH=\sqrt{64}=8\)

a) xét ▲ABD VÀ▲ EBD có

BD là cạnh chung

góc ABD= góc DBE

AB= BE

nên Δ ABD=Δ EBD (c.g.c)

b) vì Δ ABD=Δ EBD (cmt)

→ góc BED= góc BAC (2 góc tương ứng)

c) ta có:

AH VUÔNG VỚI BC

→ góc AHE = 90^{o (}1)

góc bed = 90^o (cmt) (2)

từ (1) và (2) suy ra DE song song với AH (2 đường thẳng cùng vuông góc với 1 đường thẳng)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

=>ΔAHB=ΔAHC

=>HB=HC và góc BAH=góc CAH

b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có

AH chung

góc MAH=góc NAH

=>ΔAMH=ΔANH

=>AM=AN

=>ΔAMN cân tại A

a) Vì \(AH\perp BC\Rightarrow\widehat{AHB}=90^o\)\(\Rightarrow\widehat{BAH}=90^o-\widehat{ABC}=90^o-60^o=30^o\)

b) Do \(AB//CD\Rightarrow\widehat{BAC}=\widehat{ACD}\)(2 góc so le trong)

\(\Rightarrow\Delta ABC=\Delta CDA\left(cgc\right)\)vì\(\hept{\begin{cases}AB=CD\\\widehat{BAC}=\widehat{ACD}\\ACchung\end{cases}}\)

c) Vì \(\Delta ABC=\Delta CDA\Rightarrow\widehat{ACB}=\widehat{CAD}\)(2 góc tương ứng)

Mà 2 góc này nằm ở vị trí so le trong của 2 đường thẳng AD và BC\(\Rightarrow AD//BC\)

Ta có \(AD//BC,AH\perp BC\Rightarrow AD\perp AH\)

mình thấy mọi người toàn hỏi hình học nhỉ