Cho đường thẳng d:y= -2+5; d':y=x+2
Tìm tọa độ giao điểm của d;d' bằng phép tính
Những câu hỏi liên quan
Cho parabol (P):y=x^2 và đường thẳng d:y= 2x+3
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : y = m x + 5.
a) Chứng minh đường thẳng (d) luôn đi qua điểm A(0;5) với mọi giá trị của m.
Thay tọa độ điểm A(0;5) vào phương trình đường thẳng d : y = m x + 5. ta được:
5=m.0+5 luôn đúng với mọi giá trị của tham số m nên đường thẳng (d) luôn
đi qua điểm A với mọi giá trị của m.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường thẳng d:y3x-2 để phép tịnh tiến theo
v
→
biến đường thẳng d thành chính nó thì: A.
v
→
(-1;-3) B.
v
→
(-1;3) C.
v
→
(3;1) D.
v
→
(3;-1)
Đọc tiếp
Trong mặt phẳng Oxy, cho đường thẳng d:y=3x-2 để phép tịnh tiến theo v → biến đường thẳng d thành chính nó thì:
A. v → =(-1;-3)
B. v → =(-1;3)
C. v → =(3;1)
D. v → =(3;-1)
cho đường thẳng d:y = (2m - 5)x - 1 + m = 0 tìm m sao cho khoảng cách từ o đến d là nhỏ nhất, lớn nhất
Cho đường thẳng d:y=(4m+5)x-2m+7 với m là tham sốa,tìm các giá trị của m để d cùng với 2 đường thẳng d1:y=3x-1 và d2:y=2x+1 đồng quyb,tìm m để d song song với d3:y=-3x+2
Xem chi tiết
a: Tọa độ giao điểm của đường thẳng (d1) và đường thẳng (d2) là:
\(\left\{{}\begin{matrix}3x-1=2x+1\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2x=2+1\\y=2x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=2\cdot3+1=7\end{matrix}\right.\)
Thay x=3 và y=7 vào (d), ta được:
\(3\left(4m+5\right)-2m+7=7\)
=>\(12m+15-2m=0\)
=>10m=-15
=>m=-3/2
b: để (d)//(d3) thì \(\left\{{}\begin{matrix}4m+5=-3\\-2m+7< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=-3-5=-8\\-2m< >-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-2\\m< >\dfrac{5}{2}\end{matrix}\right.\)
=>m=-2
Đúng 3
Bình luận (0)
a) Đường thẳng d:y frac{1}{2} cắt đồ thị hàm số y sin x,x in left[ { - pi ;pi } right] tại hai giao điểm {A_0},{B_0} (Hình 34). Tìm hoành độ của hai giao điểm {A_0},{B_0}.b) Đường thẳng d:y frac{1}{2} cắt đồ thị hàm số y sin x,x in left[ {pi ;3pi } right] tại hai giao điểm {A_1},{B_1} (Hình 34). Tìm hoành độ của hai giao điểm {A_1},{B_1}.
Đọc tiếp
a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({A_0},{B_0}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_0},{B_0}\).
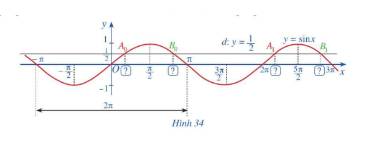
b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \sin x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({A_1},{B_1}\) (Hình 34). Tìm hoành độ của hai giao điểm \({A_1},{B_1}\).
a) Hoành độ của \({A_0}\) là \(\frac{\pi }{6}\)
Hoành độ của \({B_0}\) là \(\frac{{5\pi }}{6}\)
b) Hoành độ của \({A_1}\) là \(\frac{{13\pi }}{6}\)
Hoành độ của \({B_1}\) là \(\frac{{17\pi }}{6}\)
Đúng 0
Bình luận (0)
a) Đường thẳng d:y frac{1}{2} cắt đồ thị hàm số y cos x,x in left[ { - pi ;pi } right] tại hai giao điểm {C_0},{D_0} (Hình 35). Tìm hoành độ giao điểm của hai giao điểm {C_0},{D_0}.b) Đường thẳng d:y frac{1}{2} cắt đồ thị hàm số y cos x,x in left[ {pi ;3pi } right] tại hai giao điểm {C_1},{D_1} (Hình 35). Tìm hoành độ giao điểm của hai giao điểm {C_1},{D_1}.
Đọc tiếp
a) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ { - \pi ;\pi } \right]\) tại hai giao điểm \({C_0},{D_0}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_0},{D_0}\).
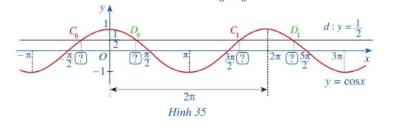
b) Đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số \(y = \cos x,x \in \left[ {\pi ;3\pi } \right]\) tại hai giao điểm \({C_1},{D_1}\) (Hình 35). Tìm hoành độ giao điểm của hai giao điểm \({C_1},{D_1}\).
a) Hoành độ của \({C_0}\) là \( - \frac{\pi }{3}\)
Hoành độ của \({D_0}\) là \(\frac{\pi }{3}\)
b) Hoành độ của \({C_1}\) là \(\frac{{5\pi }}{3}\)
Hoành độ của \({D_1}\) là \(\frac{{7\pi }}{3}\)
Đúng 0
Bình luận (0)
Tìm m để 2 đường thẳng d:y = 5x+m-3;d':y =3x+5-m cắt nhau tại 1 điểm nằm trên trục tung
\(=>m-3=5-m=>m=4\)
\(5\ne3\) (luôn đúng)
Vậy m=4 thì..............
Đúng 0
Bình luận (0)
Phương trình hoành độ giao điểm :
\(5x+m-3=3x+5-m\)
\(\Leftrightarrow2x=-2m+8\left(1\right)\)
Cắt nhau tại điểm điểm nằm trên trục tung
=> Điểm có hoành độ là 0
\(\left(1\right):-2m+8=0\)
\(\Leftrightarrow m=4\)
Đúng 1
Bình luận (0)
Cho đường thẳng \(d:y = - x - 2022\). Xác định hai hàm số biết đồ thị của chúng là hai đường thẳng cắt \(d\).
Đường thẳng \(d:y = - x - 2022\) có \(a = - 1;b = - 2022\).
- Gọi \({d_1}:y = {a_1}x + {b_1}\) là đường thẳng cần tìm thứ nhất. Vì \({d_1}\) cắt \(d\) nên \(a \ne {a_1} \Rightarrow - 1 \ne {a_1}\) và \({b_1}\) tùy ý. Ta chọn \({a_1} = 5;{b_1} = 4\)
Ta có đường thẳng \({d_1}:y = 5x + 4\).
Vậy hàm số thứ nhất cần tìm là \(y = 5x + 4\)
- Gọi \({d_2}:y = {a_2}x + {b_2}\) là đường thẳng cần tìm thứ hai. Vì \({d_2}\) cắt \(d\) nên \(a \ne {a_2} \Rightarrow - 1 \ne {a_2}\) và \({b_2}\) tùy ý. Ta chọn \({a_2} = 25;{b_2} = 5\)
Ta có đường thẳng \({d_2}:y = 25x + 5\).
Vậy hàm số thứ hai cần tìm là \(y = 25x + 5\).
Đúng 0
Bình luận (0)