Điểm điều tra về chất lượng sản phẩm mới (thang điểm 100) như sau:
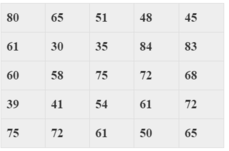
Mod của bảng số liệu trên là:
A. Mo = 3
B. Mo = 61
C. Mo = 61; Mo = 72
D. Mo = 72
Điểm điều tra về chất lượng sản phẩm mới ( thang điểm 100) như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 68 39 41 54 61 72 75 72 61 50 65 72
Tìm mốt của bảng số liệu trên.
A. 61
B. 72
C. 75
D. Đáp án khác
Chọn D.
Ta có bảng phân bố tần số:
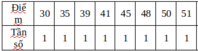
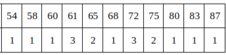
Bảng trên có 2 số có tần số lớn nhất là 61 và 72.
Vậy mẫu số liệu trên có hai mốt là M0= 61 và M0 = 72.
Điểm điều tra về chất lượng sản phẩm mới ( thang điểm 100) như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 68 39 41 54 61 72 75 72 61 50 65 72
Tính số trung vị của dãy số liệu trên
A. 58
B. 61
C. 68
D. 75
Chọn D.
Sắp sếp lại số liệu trên theo thứ tự tăng dần của điểm số

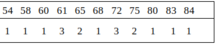
Vì n = 25 là số lẻ nên số trung vị là số đứng ở vị trí thứ 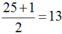
Do đó số trung vị là: Me= 75.
Người ta tiến hành phỏng vấn một số người về chất lượng của một loại sản phẩm mới. người điều tra yêu cầu cho điểm sản phẩm ( thang điểm 100) kết quả như sau:
80 65 51 48 45 61 30 35 84 83 60 58 75 68 39 41 54 61 72 75 72 61 58 65 72
Hỏi phương sai gần với số nào nhất. Nhận xét gì về các kết quả nhận được.
A. 215
B. 216
C. 217
D. 218
Chọn C.
Ta lập bảng phân bố tần số như sau:
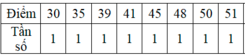

Ta có:

Người ta tiến hành phỏng vấn 40 người về một mẫu áo sơ mi mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm là 100. Kết quả được trình bày trong Bảng 16.
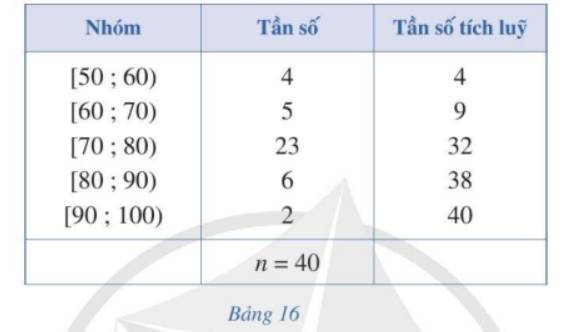
a) Trung vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị:
A. 74
B. 75
C. 76
D. 77
b, Tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. \({Q_1} \approx 71;{Q_2} \approx 76;{Q_3} \approx 78\)
B. \({Q_1} \approx 71;{Q_2} \approx 75;{Q_3} \approx 78\)
C. \({Q_1} \approx 70;{Q_2} \approx 76;{Q_3} \approx 79\)
D. \({Q_1} \approx 70;{Q_2} \approx 75;{Q_3} \approx 79\)
c, Mốt của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng đơn vị) là:
A. 73
B. 74
C. 75
D. 76
a,
Trung vị: \({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 70 + \left( {\frac{{20 - 9}}{{23}}} \right).10 = \frac{{1720}}{{23}} \approx 74,8\)
⇨ Chọn: B. 75
b,
- Tứ phân vị thứ hai \({Q_2} = {M_e} = 75\) => Loại A, C
- Tứ phân vị thứ nhất: \({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 70 + \left( {\frac{{10 - 9}}{{23}}} \right).10 = \frac{{1620}}{{23}} \approx 70\)
⇨ Chọn D
c,
\({M_o} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 70 + \left( {\frac{{23 - 5}}{{2.23 - 5 - 6}}} \right).10 = \frac{{526}}{7} \approx 75\)
⇨ Chọn C
Xác định CTHH của
a) Oxit sắt có mFe : mo = 21:8
b) Hợp chất có % Ca : %C : %O = 10:3:12 theo khối lượng
c) Tỉ lệ khối lượng mMg : mC : mO = 2:1:4
Tìm số nguyên tử của mỗi nguyên tố trong 8,4g hợp chất trên
b)
%Ca : %C : %O = 10 :3 : 12
=> 40.nCa : 12.nC : 16.nO = 10 : 3 : 12
=> nCa : nC : nO = 1 : 1 : 3
=> CTHH: CaCO3
c)
24.nMg : 12.nC : 16.nO = 2:1:4
=> nMg : nC : nO = 1 : 1 : 3
=> CTHH: MgCO3
\(n_{MgCO_3}=\dfrac{8,4}{84}=0,1\left(mol\right)\)
=> Số nguyên tử Mg = 0,1.1.6.1023 = 0,6.1023
=> Số nguyên tử C = 0,1.1.6.1023 = 0,6.1023
=> Số nguyên tử O = 0,1.3.6.1023 = 1,8.1023
a: Theo đề, ta có:
\(\dfrac{n_{Fe}\cdot56}{n_O\cdot16}=\dfrac{21}{8}\Leftrightarrow\dfrac{n_{Fe}}{n_O}=\dfrac{3}{4}\)
Vậy: Công thức là \(Fe_3O_4\)
16. Cho ΔABC vuông tại A có AB<AC và trung tuyến AM.
a, Cm ΔAMC cân
b, Từ M hạ MO⊥AC. Trên tia MO lấy N sao cho MO=NO. Cm AMCN là hình thoi
c, Gọi I là trung điểm của MC và D là điểm trên tia NI sao cho IN=ID. Cm 3 điểm A,M,D thẳng hàng
a: ΔABC vuông tại A có AM là trung tuyến
nên MA=MC=MB
=>ΔMAC cân tại M
b: Xét tứ giác AMCN có
O là trung điểm chung của AC và MN
=>AMCN là hình bình hành
mà MA=MC
nên AMCN là hình thoi
c: Xét tứ giác MNCD có
I là trung điểm chung của MC và ND
=>MNCD là hình bình hành
=>MD//CN
mà CN//AM
nên A,M,D thẳng hàng
Người ta điều tra sản phẩm của hai tổ đóng gói các túi đường (có khối lượng quy định là 2kg). Kết quả điều tra cho các số liệu thống kê ghi ở hai bảng sau :

a) Lập bảng phân bố tần số và tần suất ghép lớp theo sản phẩm của tổ A với các lớp
[1,90; 1,98); [1,98; 2,06); [2,06; 2,14); [2,14; 2,22); [2,22; 2,30]
b) Lập bảng phân bố tần số và tần suất ghép lớp theo sản phẩm của tổ B vói các lớp
[1,5; 1,7); [1,7; 1,9); [1,9; 2,1); [2,1; 2,3); [2,3; 2,30]
c) Tính số trung bình, phương sai và độ lệch chuẩn của các số liệu thống kê cho ở bảng 15, bảng 16. Từ đó, xét xem trong lần điều tra này, sản phẩm của tổ nào có khối lượng đồng đều hơn ?
Bài 2: Điểm kiểm tra học kỳ môn toán của một nhóm 30 h/s lớp 7 được ghi lại như sau:
1 2 3 4 5 6 7 8 9 10
1 1 2 3 9 8 7 5 2 2 N = 40
a) Dấu hiệu ở đây là gì?
b) Lập bảng tần số và tính trung bình cộng của bảng số liệu trên.
c) Nhận xét chung về chất lượng học của nhóm h/s đó.
d) Vẽ biểu đồ đoạn thẳng.
Cho góc nhọn xOy, trên tia Ox lấy điểm A (A khác 0), trên tia Oy lấy điểm B sao cho OA = OB. Gọi M là trung điểm của đoạn thẳng AB.
1) Chứng minh tam giác AΟΜ = tam giác BOM.
2) Trên tia đối của tia MO, lấy điểm N sao cho MN = MO. Chứng minh NAM = OBM.
3) Gọi K là trung điểm của đoạn thẳng OB, H là trung điểm của đoạn thẳng AN. Chứng minh ba điểm H, M, K là ba điểm thẳng hàng.
1: Xét ΔAOM và ΔBOM có
OA=OB
OM chung
AM=BM
Do đó: ΔOAM=ΔOBM
2: Xét ΔMNA và ΔMOB có
MN=MO
\(\widehat{NMA}=\widehat{OMB}\)(hai góc đối đỉnh)
MA=MB
Do đó: ΔMNA=ΔMOB
3: Ta có: ΔMNA=ΔMOB
=>NA=OB
Ta có: ΔMNA=ΔMOB
=>\(\widehat{MNA}=\widehat{MOB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//OB
Ta có: OB=AN
\(OK=KB=\dfrac{OB}{2}\)(K là trung điểm của OB)
\(AH=HN=\dfrac{AN}{2}\)(H là trung điểm của AN)
Do đó: OK=KB=AH=HN
Xét tứ giác OKNH có
OK//NH
OK=NH
Do đó: OKNH là hình bình hành
=>ON cắt KH tại trung điểm của mỗi đường
mà M là trung điểm của ON
nên M là trung điểm của KH
=>K,M,H thẳng hàng