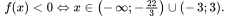§4. Phương sai và độ lệch chuẩn

\(=\dfrac{4}{9}x^6y^4\cdot\dfrac{1}{2}x^2y^5=\dfrac{2}{9}x^8y^9\)

cách 1:

ta có : \(\overline{x}=\dfrac{1}{N}\sum\limits^m_{i=1}x_in_i=\dfrac{x_1n_1+x_2n_2+...+x_mn_m}{N}\)

\(\Leftrightarrow\overline{x}=\dfrac{8.2+5.15+2.3+6.10}{30}\simeq5,23\)

\(\Rightarrow S^2=\dfrac{1}{N}\sum\limits^N_{i=1}n_i\left(x_i-\overline{x}\right)^2=\dfrac{2.\left(8-5,23\right)^2+15.\left(5-5,23\right)^2+3.\left(2-5,23\right)^2+10.\left(6-5,23\right)^2}{30}\)

\(\Leftrightarrow S^2=1,7789\)

cách 2 :

ta có : \(S^2=\dfrac{1}{N}\sum\limits^N_{i=1}x_in_i-\dfrac{1}{N^2}\left(\sum\limits^N_{i=1}x_in_i\right)^2\)

thế số vào tính là ra

Bất phương trình tương đương với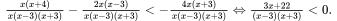

Đặt 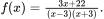 Ta có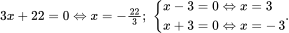 
Bảng xét dấu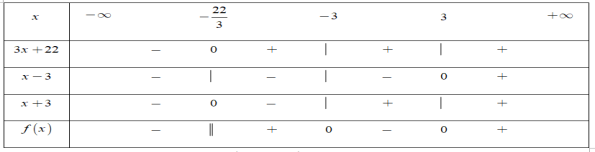

Dựa vào bảng xét dấu, ta thấy rằng