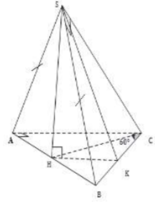
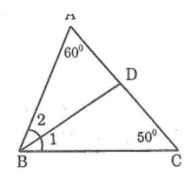
Cho tam giác ABC vuông ở C và có góc A = 60o; Kẻ tia phân giác AE của góc CAB. Gọi K là hình chiếu của điển E trên cạnh AB. Kẻ tia Bx vuông góc với tia AE ở D. Chứng minh rằng
a) tam giác ACE = tam giác AKE
b) EB > AC
c) Ba đường thẳng AC, BD, KE cùng đi qua 1 điểm