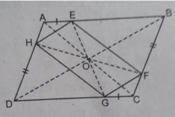
Cho hình bình hành ABCD. Trên các cạnh AB; BC; CD; DA lấy các điểm E; F; G; H sao cho AE = CG; BF = DH. CMR:
a, Xác định tâm đối xứng của hình bình hành ABCD
b, EFGH là hình bình hành và tìm tâm đối xứng
c, Gọi O là giao điểm của AC và BD, O còn là tâm đối xứng của hình bình hành nào?