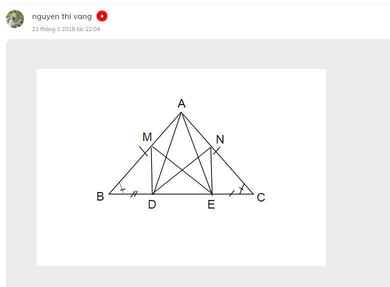
Cho ΔABC cân ở A. Lấy DE ∈ BC sao cho BD=CE < \(\frac{BC}{2}\). Kẻ DM⊥BC (M ∈AB); EN ⊥BC (N ∈ AC)
Chứng minh:
a, DM=EN
b, EM=DN
c,ΔADE cân

Những câu hỏi liên quan
Cho ΔABC cân tại A. Trên cạnh AB lấy điểm D. Trên tia đối của tai AC lấy điểm E sao cho BD=CE, nối D với E sao cho BD=CE, nối D với E, kẻ DH vuông góc với BC (H thuộc BC), EK vuông góc với BC (K thuộc BC). chứng minh:
a) BH=CK
b) BC<DE
a: Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
góc DBH=góc ECK
=>ΔDHB=ΔEKC
=>BH=CK
b: Tham khảo:

Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D,E sao cho BD=CE<BC/2. Đường thẳng kẻ từ D vuông góc với BC cắt AB ở M, đường thẳng kẻ từ E vuông góc với BC cắt AC ở N. Chứng minh rằng:
a) DM=EN
b) EM=DN
c) Chứng minh tam giác ADE cân.
Cho ΔABC cân tại A, M là trung điểm của AB. Trên tia đối tia MC lấy điểm D sao cho DM = MC. Kẻ MN // BC (N ϵ AC). Gọi H là trung điểm của BC, 2 đường thẳng BN và AD cắt nhau tại E. Chứng minh 3 đường thẳng AH,BD,CE cùng đi qua một điểm.
Xét tứ giác ADBC có
M la trung điểm chung của AB và DC
nên ADBC là hình bình hành
=>góc ADB=góc ACB
Xét ΔABC có
MN//BC
AM/AB=1/2
=>N là trung điểm của AC
Xét ΔNBC và ΔNEA có
góc NCB=góc NAE
NC=NA
góc BNC=góc ENA
=>ΔNBC=ΔNEA
=>NB=NE
=>AECB là hình bình hành
=>CE=AB=AC=BD và góc AEC=góc ABC
=>góc AEC=góc ADB
Gọi giao của BD và CE là K
Xét ΔKDE có góc KDE=góc KED
nên ΔKDE cân tại K
=>KD=KE
=>KB=KC
=>K nằm trên trung trực của BC
mà AH là trung trực của BC
nên A,H,K thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC cân ở A . Trên cạnh BC lấy 2 điểm D và E sao cho BD=CE nhỏ hơn BC/2 . Kẻ đoạn thẳng từ D vuông góc với BC cắt AB ở M , kẻ đoạn thẳng từ E vuông góc với BC cắt AC ở N . Chứng minh rằng : a) DM=EN. b)EM =DN. c)Tam giác ADE cân
Cho tam giác cân ABC có AB= AC. Trên tia đối của tia BA và CA lấy hai điểm D và E sao cho BD = CE.
a) C/m DE // BCH
b) Từ D kẻ DM vuông góc với BC tại M, từ E kẻ EN vuông góc với BC tại N. C/m DM = EN.
c) C/m tam giác AMN là tam giác cân.
d) Từ B và C kẻ các đường vuông gócvới AM và AN chúng cắt nhau tại I. C/m AI là tia phân giác chung của góc BAC và góc MAN
Xem chi tiết
a) Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(1)
Ta có: AD=AB+BD(B nằm giữa A và D)
AE=AC+CE(C nằm giữa A và E)
mà AB=AC(ΔABC cân tại A)
và BD=CE(gt)
nên AD=AE
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
Ta có: ΔADE cân tại A(cmt)
nên \(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔADE cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}=\widehat{ADE}\)
mà \(\widehat{ABC}\) và \(\widehat{ADE}\) là hai góc ở vị trí đồng vị
nên BC//DE(Dấu hiệu nhận biết hai đường thẳng song song)
b) Ta có: \(\widehat{DBM}=\widehat{ABC}\)(hai góc đối đỉnh)
\(\widehat{ECN}=\widehat{ACB}\)(hai góc đối đỉnh)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{DBM}=\widehat{ECN}\)
Xét ΔDBM vuông tại M và ΔECN vuông tại N có
BD=CE(gt)
\(\widehat{DBM}=\widehat{ECN}\)(cmt)
Do đó: ΔDBM=ΔECN(cạnh huyền-góc nhọn)
nên DM=EN(hai cạnh tương ứng)
c) Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
BM=CN(ΔDBM=ΔECN)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACN(c-g-c)
nên AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
Đúng 3
Bình luận (0)
cho tam giác abc cân tại a. trên bc lấy d và e sao cho bd=ce<\(\frac{1}{2}\)bc
a, cmr tam giác ade cân
b, kẻ dm vuông góc với ab tại m. gọi i là giao điểm của dm và en. cmr ai là tia phân giác của góc dae
c, gọi k là giao điểm của ai và de . tính ak khi ad=13cm; de=10cm
Bài 2: Cho tam giác ABC cân ở A. Trên cạnh BC lấy D, trên tia đối của tia CB lấy E sao cho BD CE. Từ D kẻ đường vuông góc với BC cắt AB ở M, từ E kẻ đường vuông góc với BC cắt AC ở N.a) Chứng minh: MD NEb) MN cắt DE ở I. Chứng minh: I là trung điểm DE.c) Từ C kẻ đường thẳng vuông góc với AC, từ B kẻ đường vuông góc với AB chúng cắt nhau ở O. Chứng minh: AO là phân giác góc BAC.d) Chứng minh: AO là trung trực BC.
Đọc tiếp
Bài 2: Cho tam giác ABC cân ở A. Trên cạnh BC lấy D, trên tia đối của tia CB lấy E sao cho BD = CE. Từ D kẻ đường vuông góc với BC cắt AB ở M, từ E kẻ đường vuông góc với BC cắt AC ở N.
a) Chứng minh: MD = NE
b) MN cắt DE ở I. Chứng minh: I là trung điểm DE.
c) Từ C kẻ đường thẳng vuông góc với AC, từ B kẻ đường vuông góc với AB chúng cắt nhau ở O. Chứng minh: AO là phân giác góc BAC.
d) Chứng minh: AO là trung trực BC.
Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D sao cho BD < DC ( D khác B, C), trên tia đối của tia CB lấy điểm E sao cho BD = CE. Từ D kẻ đường vuông góc với BC cắt AB ở M, từ E kẻ đường vuông góc với BC cắt AC ở N. Đoạn thẳng MN cắt DE ở I. Chứng minh
1. Tam giác MDB = tam giác NEC
2. I là trung điểm của DE
3. BC < MN
B=(2.4.10+4.6.8+14.16.20)/(3.6.15+6.9.12+21.24.30)
Đúng 0
Bình luận (0)
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
tam giác abc cân tại a. trên bc lấy e và d sao cho bd=ce<bc:2.đường thẳng kẻ từ d vuông góc với bc cắt ab ở m . đường thẳng kẻ từ e vuông góc với bc cắt ac ở n. cmr
a. dm=en
b. em=dn
c. tam giác abc cân
giúp vs. chìu kiểm tra rồi