Cho tam giác ABC cân tại A. Các đường phân giác BD và CE cắt nhau tại I (D thuộc AC; E thuộc AB). C/minh:
a, BD = CE
b, AI là phân giác của góc A
c, BE = ED = DC
Những câu hỏi liên quan
cho tam giác ABC nội tiếp đường tròn (O) , BD và CE lần lượt là các tia phân giác xủa góc ABC , ACB ( D , E thuộc (O) ) cắt nhau tại I . DE cắt AB , AC tại M, N . Chứng minh Tam giác AMN cân và tam giác AID cân
( vẽ hình giúp em với ạ )
Ta có CE là tia phân giác của ACB
=> góc ACE= góc BCE
=> cung AE= cung BE
Ta có BD là tia phân giác góc ABC
=> góc ABD= góc DBC
=> cung AD= cung DC
Ta có góc AMN=
( cung AD+ EB)
góc ANM=( cung DC+ AE)
mak cung AE= cung BE và cung AD= cung DC
=> góc AMN= góc ANM=> tam giác AMN cân
Ta có BD là đường phân giác thứ 1 (gt)
CE là đường phân giác thứ 2(gt)
mak BD giao CE tại I
=> I là trọng tâm
=> AI là đường phân giác thứ 3
=> góc BAI= góc IAC
Ta có góc IAD= góc IAC+góc CAD
mak góc IAC=góc BAI(cmt) và góc CAD= góc ABI(vì góc CAD chắn cung DC và góc ABI chắn cung AD mak cung AD= cung DC (cmt) )
=>góc IAD=góc BAI+góc ABI(1)
Ta cso góc AID là góc ngoài của tam giác ABI
=> góc AID= góc BAI+góc ABI(2)
từ (1) và (2) =>góc IAD= góc AID
=> tam giác AID cân
Đúng 0
Bình luận (0)
Tớ làm lại nha cái kia bị lỗi với lại là cậu tự vẽ hình nha tớ vẽ hình gửi vào đây nó bị lỗi k hiện á
Ta có CE là tia phân giác của ACB
=> góc ACE= góc BCE
=> cung AE= cung BE
Ta có BD là tia phân giác góc ABC
=> góc ABD= góc DBC
=> cung AD= cung DC
Ta có góc AMN=\(\dfrac{1}{2}\)( cung AD+ EB)
góc ANM=\(\dfrac{1}{2}\)( cung DC+ AE)
mak cung AE= cung BE và cung AD= cung DC
=> góc AMN= góc ANM=> tam giác AMN cân
Ta có BD là đường phân giác thứ 1 (gt)
CE là đường phân giác thứ 2(gt)
mak BD giao CE tại I
=> I là trọng tâm
=> AI là đường phân giác thứ 3
=> góc BAI= góc IAC
Ta có góc IAD= góc IAC+góc CAD
mak góc IAC=góc BAI(cmt) và góc CAD= góc ABI(vì góc CAD chắn cung DC và góc ABI chắn cung AD mak cung AD= cung DC (cmt) )
=>góc IAD=góc BAI+góc ABI(1)
Ta cso góc AID là góc ngoài của tam giác ABI
=> góc AID= góc BAI+góc ABI(2)
từ (1) và (2) =>góc IAD= góc AID
=> tam giác AID cân
Đúng 0
Bình luận (0)
Cho tam giác abc cân tại a, hai đường cao BD và CE cắt nhau tại I (d thuộc ac; e thuộc ab).
a) cm BD = CE.
b) CM : tam giác AED là tam giác cân và ed // bc.
c) Biết góc BAC = 70 độ. tính các góc của tam giác ibc.
d) Qua b kẻ tia Bx//CE; qua C kẻ Cy //bd. Bx và Cy cắt nhau tại M. cm IM đi qua trung điểm của BC.
Cho tam giác ABC cân tại A, biết AB = AC = 6cm, BC = 4cm. Các đường phân giác BD, CE cắt nhau tại I ( E thuộc AB ; D thuộc AC)
a. Tính AD, DC , DE
B. Cm : tam giác IDC đồng dạng CDB
c. Tính BD , CE
cho tam giác abc cân tại a, 2 đường cao bd và ce cắt nhau tại i (d thuộc ac, e thuộc ab).
a) cm bd = ce.
b) cm tam giác aed là tam giác cân và ed // bc.
c) biết góc bac bằng 70 độ. tính các góc của tam giác ibc.
d) qua b kẻ tia Bx // CE, qua c kẻ tia Cy // BD, Bx và Cy cắt nhau tại m. chứng minh rằng im đi qua trung điểm của bc.
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Suy ra: BD=CE(hai cạnh tương ứng)
Đúng 1
Bình luận (0)
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
Đúng 1
Bình luận (0)
b) Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(1)
Ta có: ΔADE cân tại A(cmt)
nên \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔADE cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AED}=\widehat{ABC}\)
mà \(\widehat{AED}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên DE//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Đúng 1
Bình luận (0)
cho tam giác abc cân tại a ha đường cao bd và ce cắt nhau tại h ( d thuộc ac; e thuộc ab a chứng minh tam giác bcd = tam giác cbe b chứng minh tam giác bhc cân chứng minh tia phân ah là tia phân giác của BAC
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
CB chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
b: Xét ΔHBC có góc HCB=góc HBC
nên ΔHBC cân tại H
c: Xet ΔABH và ΔACH có
AB=AC
BH=CH
AH chung
=>ΔABH=ΔACH
=>góc BAH=góc CAH
=>AH làphân giác của góc BAC
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A ( A < 90 độ ) . Kẻ BD vuông góc Ac ( D thuộc AC ) , CE vuông góc AB ( E thuộc AB ) , BD và CE cắt nhau tại H . a, CM : BD = CE . b, CM : tam giác BHC cân . c, CM : AH là đường trung trực của BC . d, TRên tia BD lấy điểm K sao cho D là trung điểm của BK . So sánh ECB và DKC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A ( góc A< 90 độ), các đường cao BD,CE (D thuộc Ac ; E thuộc AB) cắt nhau tại H .
a) Chứng minh BD = CE
.b) Chứng minh tam giác BHC là tam giác cân.
c) So sánh HB và HD.
20 tháng 4 2022 lúc 21:11
a)cho tam giác ABC có các đường cao BD và CE bằng nhau . Chứng minh rằng tam giác đó là một tam giác cân
b)Cho tam giác ABC cân tại A,đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC
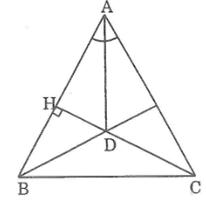
Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.
Suy ra: AD ⊥ BC
Ta có: CH ⊥ AB (gt)
Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC
Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.
Vậy BD ⊥ AC.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AB = AC = 6cm ; BC = 4cm . Các đường phân giác BD và CE cắt nhau tại I ( E trên AB và D trên AC )
a) Tính độ dài AD , ED
b) Cm : Tam giác ADB đồng dạng với tam giác AEC
c) Cm : IE.CD = ID.BE
d) Cho \(S_{ABC}\) = 60 \(cm^2\) . Tính \(S_{AED}\)
b: Xét ΔADB và ΔAEC có
\(\widehat{A}\) chung
\(\widehat{ABD}=\widehat{ACE}\left(=\dfrac{1}{2}\widehat{ABC}\right)\)
Do đó: ΔADB\(\sim\)ΔAEC
Đúng 0
Bình luận (1)