Cho hình vẽ biết AE vuông góc BC, AC = 13cm, AE=12cm; BC=14cm. Tính EC và AB

Những câu hỏi liên quan
Cho AABC vuông tại A. Biết AB = 9cm, AC = 12cm. a) Tính BC?. b) Vẽ BD là tia phân giác của góc ABC cắt AC tại D. Từ D vẽ DE vuông góc với BC tại E. Cm: AABD = AEBD. c) Chứng minh: AE 1 BD. d) Kéo dài ED cắt BA tại F. Chứng minh: AE // FC.
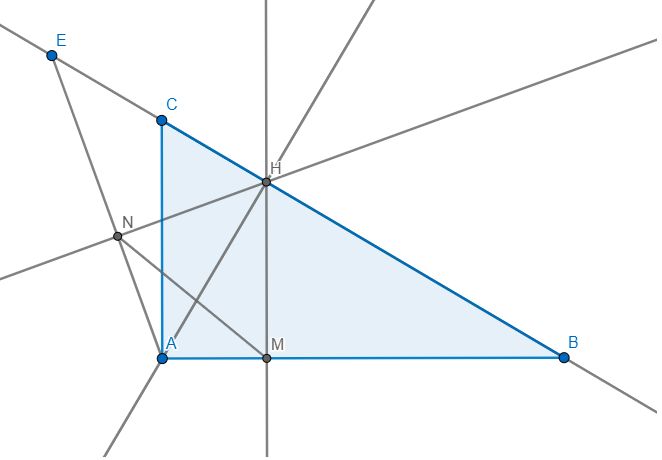
Cho tam giác ABC vuông tại A có AB= 16cm ;AC =12cm, đường cao AH. Trên tia đối của tia CB lấy điểm E. Vẽ HN vuông góc với AE tại N. a) Tính BC; AH;HB và số đo góc B b) Chứng minh AN.AE = HB .HC c) Vẽ HM vuông góc với AB tại M. Chứng minh :AE = 3 AM biết rằng BE =3 MN
a) Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{16^2+12^2}=20\left(cm\right)\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.16}{20}=\dfrac{48}{5}\left(cm\right)\)
Ta có: \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{16^2}{20}=\dfrac{64}{5}\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\Rightarrow\angle B\approx37\)
b) tam giác AHE vuông tại H có HN là đường cao \(\Rightarrow AN.AE=AH^2\)
tam giác ABC vuông tại A có AH là đường cao \(\Rightarrow AH^2=HB.HC\)
\(\Rightarrow AN.AE=HB.HC\)
c) tam giác AHB vuông tại H có HM là đường cao \(\Rightarrow AH^2=AM.AB\)
\(\Rightarrow AN.AE=AM.AB\Rightarrow\dfrac{AM}{AE}=\dfrac{AN}{AB}\)
Xét \(\Delta AMN\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle EABchung\\\dfrac{AM}{AE}=\dfrac{AN}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta AEB\left(c-g-c\right)\Rightarrow\dfrac{AE}{AM}=\dfrac{BE}{MN}\)
mà \(BE=3MN\Rightarrow\dfrac{BE}{MN}=3\Rightarrow\dfrac{AE}{AM}=3\Rightarrow AE=3AM\)
Đúng 2
Bình luận (1)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot20=16\cdot12=192\)
hay AH=9,6(cm)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=16^2-9.6^2=163.84\)
hay HB=12,8(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\)
hay \(\widehat{B}\simeq37^0\)
Đúng 0
Bình luận (0)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHE vuông tại H có HN là đường cao ứng với cạnh huyền AE, ta được:
\(AN\cdot AE=AH^2\)(2)
Từ (1) và (2) suy ra \(HB\cdot HC=AN\cdot AE\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có AB=10cm, BC=12cm. Vẽ phân giác góc A cắt BC tại D
A, chứng minh tam giác ABD = tam giác ACM
B, tính AD, so sánh góc BAC và góc ABC
C, vẽ DE vuông góc AB (E thuộc AB) DF vuông góc AC (F thuộc AC). Chứng minh AF bằng AE và EF//BC.
Cho mình cả hình vẽ nha, minh cảm ơn
Mọi người trả lời giùm minh đi minh đang có viêc gâp
Đúng 0
Bình luận (0)
a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A =90 độ vẽ AD vuông góc với AB (D,C nằm khác phía với A,B) và AD=AB. Vẽ AE vuông góc với AC (E,B nằm khác phía đối với AC) và AE=AC , biết DE=BC . Tính góc BAC
Cho tam giác nhọc ABC . qua A vẽ AH vuông góc BC(Hthuộc Bc).Từ H vẽ HKvuông góc AC ( Kthuộc AC). Qua K vẽ Đường ThẳnG sog sog BC cắt AB tại E
a) Hãy chỉ ra các cặp góc bằng nhau trên hình vẽ? giải thích?
b)Chứng minh AHvuông góc Ek
c)Qua A vẽ AD vuông góc AB sao cho AD=AB Và vẽ AE vuông góc AC sao cho AE=AC( không chứa Bvà C). chứng minh BE=DC
Cho hình vẽ biết AD vuông góc DC DCvuông góc BC BC 13cm AC= 15cm DC= 12cm tính độ dài đoạn thẳng BC
Cho tam giác ABC có góc A=90 độ. Vẽ AD vuông góc với AB(D,C nằm khác phía đối với AB) và AD = AB. Vẽ AE vuông góc với AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.
Cho tam giác ABC có góc A=90 độ. Vẽ AD vuông góc với AB(D,C nằm khác phía đối với AB) và AD = AB. Vẽ AE vuông góc với AC (E, B nằm khác phía đối với AC) và AE = AC. Biết DE = BC. Tính góc BAC.
1. cho tam giác ABC, đường cao AH6cm. tỉ số cạnh góc vuông AB:AC3:7. tình BH và HC2. cho hình vuông ABCD, lấy E thuộc BC. Tia AE cắt đường thẳng CD tại G. Trên nửa mặt phẳng B là đường thẳng AE chưa tia AD, kẻ AF vuông góc với AE và AFAE. Chứng minha, F,C,D thẳng hàngb, 1/AD^21/AE^2+1/AG^2c, Biết AD13cm, AF:AG10:13. TÍnh FG3. Cho tam giác ABC, góc B 60 độ, BC8cm, AB+AC12cm.TÍnh AB
Đọc tiếp
1. cho tam giác ABC, đường cao AH=6cm. tỉ số cạnh góc vuông AB:AC=3:7. tình BH và HC
2. cho hình vuông ABCD, lấy E thuộc BC. Tia AE cắt đường thẳng CD tại G. Trên nửa mặt phẳng B là đường thẳng AE chưa tia AD, kẻ AF vuông góc với AE và AF=AE. Chứng minh"
a, F,C,D thẳng hàng
b, 1/AD^2=1/AE^2+1/AG^2
c, Biết AD=13cm, AF:AG=10:13. TÍnh FG
3. Cho tam giác ABC, góc B = 60 độ, BC=8cm, AB+AC=12cm.TÍnh AB
Cho tam giác ABC vuông tại A có AB=16cm, AC=12cm. a) tính BC. b) vẽ AH vuông góc với BC tại H, trên HB lấy E sao cho HE=HC. chứng minh AC=AE. c) Trên tia đối tia HA lấy D sao cho DH=AH. chứng minh ED vuông góc AB. d) chứng minh CH<AH


















