Tính: A=12+32+52+...+(2n-1)2 ; B=13+33+53+...+(2n-1)3

Những câu hỏi liên quan
Tính:
a)
\(A =\) \({12 + 32 + 52 + ... + (2n-1) ^ 2}\)
b)
\(B = {13 + 33 + 53 + …+ (2n -1) ^3 }\)
tổng số số hạng của dãy là: \(\left(\left(2n-1\right)^2-12\right):20+1\)chia 20 vì mỗi phần tử cách nhau 20 đơn vị
tổng của dãy : \(\frac{\left(\left(\left(2n-1\right)^2-12\right):20+1\right)\times\left(\left(2n-1\right)^2+12\right)}{2}\)
bài b tương tự ạ
Đúng 0
Bình luận (0)
Viết chương trình tính tổng sau S=1+32+52+72+....+(2n-1)2
Pascal
uses crt;
var i,n,s:longint;
begin
clrscr;
readln(n);
s:=0;
for i:=1 to n do
s:=s+sqr((2*i-1));
writeln(s);
readln;
end.
Đúng 1
Bình luận (0)
Chứng minh đẳng thức sau (
v
ớ
i
n
∈
N
∗
)
1
2
+
3
2
+
5
2
+
.
.
.
+
2...
Đọc tiếp
Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 1 2 + 3 2 + 5 2 + . . . + 2 n - 1 2 = n 4 n 2 - 1 3
Đặt vế trái bằng S n
Với n = 1 vế trái chỉ có một số hạng bằng 1, vế phải bằng 1
Giả sử đã có 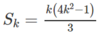 với k ≥ 1. Ta phải chứng minh
với k ≥ 1. Ta phải chứng minh
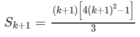
Thật vậy, ta có
S k + 1 = S k + 2 k + 1 - 1 2 = S k + 2 k + 1 2
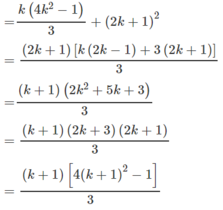
Đúng 0
Bình luận (0)
Bỏ dấu ngoặc rồi tính:
1)(15+37)+(52-17-37)
2)(21-32)-(-12+32)
\(\text{1.(15+37)+(52-17-37)}\\ =15+37+52-17-37\\ =\left(15+52-17\right)+\left(37-37\right)\\ =50+0=50\)
\(\text{2.(21-32)-(-12+32)}\\ =21-32+12-32\\ =\left(21+12\right)+\left(-32-32\right)\\ =33+-64=-31\)
Đúng 1
Bình luận (1)
\(1,=15+37+52-17-37=50\)
\(2,=21-32+12-32=-40\)
Đúng 0
Bình luận (1)
Cho B=12-22+32-42+...+(2n+1)2-(2n)2. a) Tính giá trị của B khi 2n =2020. b) Tìm n lớn nhất và B,để B<1000.
Tính nhanh :
a) 125.(-61).(-23).(-1)2n n thuộc N*
b) (-125).(+25).(-32).(-14)
c) (-31).(+52)+(-26).(-162)
61000
-1400000
2600
Cách làm là...........bấm máy tính hjhj
Đúng 0
Bình luận (0)
Bài 1: Tính: A31+33+35+37+...+3111 B32+34+36+...+3200 C51+53+55+...+599 D 52+54+56+...+5100Bài 2: Chứng minh các phân số sau tối giản với n ϵ Na) dfrac{2n+1}{n+1} b)dfrac{2n+3}{3n+4}
Đọc tiếp
Bài 1: Tính: A=31+33+35+37+...+3111
B=32+34+36+...+3200
C=51+53+55+...+599
D= 52+54+56+...+5100
Bài 2: Chứng minh các phân số sau tối giản với n ϵ N
a) \(\dfrac{2n+1}{n+1}\) b)\(\dfrac{2n+3}{3n+4}\)
Bài 1:
1) \(9A=3^3+3^5+...+3^{113}\)
\(\Rightarrow8A=9A-A=3^3+3^5+...+3^{113}-3-3^3-...-3^{111}=3^{113}-3\)
\(\Rightarrow A=\dfrac{3^{113}-3}{8}\)
2) \(9B=3^4+3^6+...+3^{202}\)
\(\Rightarrow8B=9B-B=3^4+3^6+...+3^{202}-3^2-3^4-...-3^{200}=3^{202}-3^2=3^{202}-9\)
\(\Rightarrow B=\dfrac{3^{202}-9}{8}\)
3) \(25C=5^3+5^5+...+5^{101}\)
\(\Rightarrow24C=25C-C=5^3+5^5+...+5^{101}-5-5^3-...-5^{99}=5^{101}-5\)
\(\Rightarrow C=\dfrac{5^{101}-5}{24}\)
4) \(25D=5^4+5^6+...+5^{102}\)
\(\Rightarrow24D=25D-D=5^4+5^6+...+5^{102}-5^2-5^4-...-5^{100}=5^{102}-25\)
\(\Rightarrow D=\dfrac{5^{102}-25}{24}\)
Đúng 1
Bình luận (0)
Bài 2:
a) Gọi d là UCLN(2n+1,n+1)
\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\n+1⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}2n+1⋮d\\2n+2⋮d\end{matrix}\right.\)
\(\Rightarrow\left(2n+2\right)-\left(2n+1\right)⋮d\Rightarrow1⋮d\)
Vậy 2n+1 và n+1 là 2 số nguyên tố cùng nhau
\(\Rightarrow\dfrac{2n+1}{n+1}\) là phân số tối giản
b) Gọi d là UCLN(2n+3,3n+4)
\(\Rightarrow\left\{{}\begin{matrix}2n+3⋮d\\3n+4⋮d\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}6n+9⋮d\\6n+8⋮d\end{matrix}\right.\)
\(\Rightarrow\left(6n+9\right)-\left(6n+8\right)⋮d\Rightarrow1⋮d\)
\(\Rightarrow\dfrac{2n+3}{3n+4}\) là phân số tối giản
Đúng 1
Bình luận (2)
tính nhanh:
a,(-25).21.(-2)^2 .(-/-3/).(-1) ^ 2n+1 (nϵN*)
b,(-5)^3.67.(-/-2^3/).(-1)^2n (nϵN*)
c,31.(-18)+31.(-81)-31
d,(-12).47+(-12).52+(-12)
Máy tính đâu,nó sinh ra là để làm gì???
Đề bài
Cho biểu thức:
A=(6−23+12)−(5+53−32)A=(6−23+12)−(5+53−32)−(3−73+52).−(3−73+52).
Hãy tính giá trị của A theo hai cách
Cách 1: Trước hết tính giá trị của từng biểu thức trong ngoặc.
Cách 2: Bỏ dấu ngoặc rồi nhóm các số hạng thích hợp.
a) Tính tổng: A= 12+22+32+...+102
b) Tính theo cách hợp lí tổng B= 52+102+152+...+502
\(A=1^2+2^2+3^2+....+10^2\\ A=1^{ }+\left(1+1\right)\cdot2+3\cdot\left(2+1\right)+.....+10\cdot\left(9+1\right)\\ A=1+2\cdot1+2+3\cdot2+3+....+10\cdot9+10\\ A=\left(1+2+3...+10\right)+\left(1\cdot2+3\cdot2+.....+10\cdot9\right)\)
Gọi 1+2+3+...+10 là P
Số số hạng là: (10 - 1) : 1 +1 = 10 (số)
P = (10+1) . 10 : 2 = 55
P = 55
Gọi \(1\cdot2+2\cdot3+....+9\cdot10\) là C
\(C=1\cdot2+2\cdot3+....+9\cdot10\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot3+....+9\cdot10\cdot3\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+....+9\cdot10\cdot\left(11-8\right)\\ 3\cdot C=1\cdot2\cdot3+2\cdot3\cdot4-1\cdot2\cdot3+.....+9\cdot10\cdot11-8\cdot9\cdot10\\ 3\cdot C=9\cdot10\cdot11\\ 3\cdot C=990\\ C=330\)
\(=>A=P+C\\ =>A=55+330\\ A=385\)
b)
\(B=5^2+10^2+15^2+...+50^2\\ B=5^2+\left(2\cdot5\right)^2+\left(3\cdot5\right)^2+....+\left(5\cdot10\right)^2\\ B=5^2+2^2\cdot5^2+3^2\cdot5^2+...+5^2\cdot10^2\\ B=5^2\cdot\left(1+2^2+3^2+....+10^2\right)\\ B=25\cdot\left(1+2^2+3^2+....+10^2\right)\)
\(\left(1+2^2+3^2+....+10^2\right)=A\)
\(=>B=25\cdot A\\ B=25\cdot385\\ B=9625\)
Đúng 3
Bình luận (0)


























