a) \({d_1}\) song song với đường thẳng \({d_2}:x + 3y + 2 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_2}\) làm vectơ pháp tuyến là \(\overrightarrow n  = \left( {1;3} \right)\)

\({d_1}\) đi qua điểm \(A(2;3)\) nên ta có phương trình tổng quát

          \(\left( {x - 2} \right) + 3.\left( {y - 3} \right) = 0 \Leftrightarrow x + 3y - 11 = 0\)

b) \({d_1}\) vuông góc với đường thẳng \({d_3}:3x - y + 1 = 0\) nên nhận vectơ pháp tuyến của đường thẳng \({d_3}\) làm vectơ chỉ phương là \(\overrightarrow u  = \left( {3; - 1} \right)\)

\({d_1}\) đi qua điểm \(B(4; - 1)\) nên ta có phương trình tham số: \(\left\{ \begin{array}{l}x = 4 + 3t\\y =  - 1 - t\end{array} \right.\)

ABM=40 ĐỘ

ACE=30 ĐỘ

=> 40+30 = 70 ĐỘ

.

Có: Góc EAC + Góc BAC + Góc MAB = Góc EAM = 180 độ ( Góc EAM là góc bẹt )

=> Góc EAC + 75 độ + Góc MAB = 180 độ

=> Góc EAC + Góc MAB = 105 độ

Xét tam giác AEC có: Góc E + Góc EAC + Góc ACE = 180 độ ( định lý )

Xét tam giác AMB có: Góc M + Góc MAB + Góc ABM = 180 độ ( định lý )

=> Góc E + Góc EAC + Góc ACE + Góc M + Góc MAB + Góc ABM = 180 độ + 180 độ = 360 độ

=> ( Góc E + Góc M ) + ( Góc EAC + Góc MAB ) + ( Góc ACE + Góc ABM ) = 360 độ

=> 90 độ + 90 độ + 105 độ + ( Góc ACE + Góc ABM ) = 360 độ

=> 285 độ + ( Góc ACE + Góc ABM ) = 360 độ

=> Góc ACE + Góc ABM = 360 độ - 285 độ

=> Góc ACE + Góc ABM = 75 độ

Vậy:...

Bạn tự ghi số liệu nhé =="

1.

\(a,\Leftrightarrow2m-1+m-2=6\Leftrightarrow3m=9\Leftrightarrow m=3\\ b,2x+3y-5=0\Leftrightarrow3y=-2x+5\Leftrightarrow y=-\dfrac{2}{3}x+\dfrac{5}{3}\)

Để \(\left(d\right)\text{//}y=-\dfrac{2}{3}x+\dfrac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2m-1=-\dfrac{2}{3}\\m-2\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{6}\\m\ne\dfrac{11}{3}\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{6}\)

\(c,x+2y+1=0\Leftrightarrow2y=-x-1\Leftrightarrow y=-\dfrac{1}{2}x-\dfrac{1}{2}\\ \left(d\right)\bot y=-\dfrac{1}{2}x-\dfrac{1}{2}\Leftrightarrow\left(-\dfrac{1}{2}\right)\left(2m-1\right)=-1\\ \Leftrightarrow\dfrac{1}{2}\left(2m-1\right)=1\Leftrightarrow m-\dfrac{1}{2}=1\Leftrightarrow m=\dfrac{3}{2}\)

2.

Gọi điểm cố định đó là \(A\left(x_0;y_0\right)\)

\(\Leftrightarrow y_0=\left(2m-1\right)x_0+m-2\\ \Leftrightarrow2mx_0+m-x_0-2-y_0=0\\ \Leftrightarrow m\left(2x_0+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x_0=-1\\x_0+y_0+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{3}{2}\end{matrix}\right.\)

\(a,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)

Ta có \(\left(d\right)\) đi qua \(A\left(-3;0\right),B\left(0;2\right)\) nên \(\left\{{}\begin{matrix}0=-3a+b\\2=0a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=2\end{matrix}\right.\)

Vậy đths là \(\left(d\right):y=\dfrac{2}{3}x+2\)

\(b,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)

Ta có hệ pt \(\left\{{}\begin{matrix}1=0a+b\\0=-a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)

Vậy đths là \(\left(d\right):y=x+1\)

a,a, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b

Ta có (d)(d) đi qua A(−3;0),B(0;2)A(−3;0),B(0;2) nên {0=−3a+b2=0a+b⇔⎧⎨⎩a=23b=2{0=−3a+b2=0a+b⇔{a=23b=2

Vậy đths là (d):y=23x+2(d):y=23x+2

b,b, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b

Ta có hệ pt {

D
<Giải thích: theo lý thuyết thì câu A và C sai. Câu B sai vì nếu mình chọn x0 khác 0 thì đồ thị hàm số đó không đi qua gốc tọa độ>

a) phương trình tổng quát của đường thẳng đi qua \(M\left(1;-2\right)\) có VTPT\(\left(2;3\right)\) là \(2\left(x-1\right)+3\left(y+2\right)=0\) \(\Leftrightarrow2x+3y+4=0\)

vì đường thẳng này nhận \(\overrightarrow{u}\left(2;3\right)\) làm VTPT \(\Rightarrow\) nó nhận \(\overrightarrow{n}\left(3;-2\right)\) làm VTCP \(\Rightarrow\) phương trình tham số của nó là \(\left\{{}\begin{matrix}x=1+3t\\y=-2-2t\end{matrix}\right.\)

b) ta có đường thẳng d nhận \(\overrightarrow{u}\left(-2;1\right)\) làm VTCP \(\Rightarrow\) nhận \(\overrightarrow{n}\left(1;2\right)\) làm VTPT

phương trình tổng quát của đường thẳng đi qua \(N\left(0;-1\right)\) và nhận \(\overrightarrow{n}\left(1;2\right)\) làm VTPT là \(1\left(x-0\right)+2\left(y+1\right)=0\Leftrightarrow x+2y+2=0\)

vì nó nhận \(\overrightarrow{u}\left(-2;1\right)\) làm VTCP \(\Rightarrow\) phương trình tham số của nó là : \(\left\{{}\begin{matrix}x=-2t\\y=-1+t\end{matrix}\right.\)

c) ta có d đi qua điểm M và N \(\Rightarrow\) nó nhận \(\overrightarrow{MN}\left(2;3\right)\) làm VTCP

\(\Rightarrow\) phương trình tham số của đường thẳng đi qua \(M\left(1;-1\right)\) và nhận \(\overrightarrow{MN}\) làm VTCP là : \(\left\{{}\begin{matrix}x=1+2t\\y=-1+3t\end{matrix}\right.\)

ta có d nhận \(\overrightarrow{MN}\left(2;3\right)\) làm VTCP \(\Rightarrow\) d nhận \(\overrightarrow{n}\left(3;-2\right)\) làm VTPT

\(\Rightarrow\) phương trình tổng quát của d là : \(3\left(x-2\right)-2\left(y-3\right)=0\Leftrightarrow3x-2y=0\)

câu d và câu e ) bn chỉ cần tìm VTPT của 2 đường thẳng đó và \(\Rightarrow\) VTCP là ra hết thôi .

gợi ý : đường thẳng \(2x-3y-3=0\) có \(\overrightarrow{u}\left(2;-3\right)\) là VTPT

đường thẳng \(x-y+5=0\) có \(\overrightarrow{n}\left(1;-1\right)\) là VTPT

Đáp án B

Phương trình đường thẳng d đi qua A ( -2; 0)  có dạng: A(x+ 2) + By= 0.

Theo giả thiết, ta có:

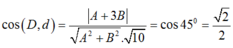
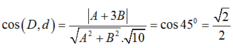
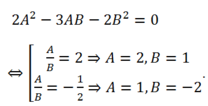
Vậy: d: 2x+ y+ 4= 0  hoặc  d: x- 2y + 2= 0.