Cho các vectơ a → = (4; -2), b → = (-1;-1), c → = (2;5). Phân tích vecto b → theo hai vecto a → và c → ta được:
A. 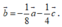
B. 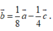
C. 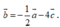
D. 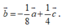
Câu 4 : Cho tam giác ABC vuông cân tại A và AB =√2 . Tính vectơ CA . vectơ BC . Câu 5 : Cho ABC có trọng tâm G . Biểu diễn vectơ AG theo hai vectơ AB , AC được kết quả là? Câu 6 : Cho các vectơ a,b thỏa mãn|vectơ a | =1 , |vectơ B | =2 , | vectơ a - vectơ b| =3 . Tích vectơ a. vectơ b bằng? Câu 7 : Cho hình vuông ABCD có cạnh bằng a . Tính| vectơ AB - vectơ AD + vectơ CD | .
Câu 4:
Áp dụng định lý Pytago
\(BC^2=AB^2+AC^2\Rightarrow BC=2\)
Ta có:
\(\overrightarrow{CA}.\overrightarrow{BC}=-\overrightarrow{CA}.\overrightarrow{CB}=-\dfrac{CA^2+CB^2-AB^2}{2}=-\dfrac{2+4-2}{2}=-2\)
Câu 5:
Gọi M là trung điểm BC
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Mà: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\)
Câu 6:
\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=3\)
\(a^2+b^2-2\overrightarrow{a}.\overrightarrow{b}=9\)
\(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1^2+2^2-9}{2}=-2\)
Câu 7:
\(\left|\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{CD}\right|=\left|\overrightarrow{DB}+\overrightarrow{CD}\right|\)
\(=\left|\overrightarrow{DB}-\overrightarrow{DC}\right|=\left|\overrightarrow{CB}\right|=BC=a\)
Cho các vectơ a → = 4 ; - 2 ; b → = - 1 ; - 1 ; c → = 2 ; 5 . Phân tích vectơ b → theo hai vectơ a → và c → , ta được:
A. b → = - 1 8 a → - 1 4 c →
B. b → = 1 8 a → - 1 4 c →
C. b → = - 1 2 a → - 4 c →
D. b → = - 1 8 a → + 1 4 c →
Trong mặt phẳng tọa độ,cho vectơ u=1/2 vectơ i -5 vectơ j và vectơ v=K vectơ i -4 vectơ j a)tìm các giá trị của K để | vectơ u|=| vectơ v| Giúp tui với mng
Cho các vectơ a(4;-2),b(m;1) . Tìm số m để hai vectơ cùng phương
Hai vecto đã cho cùng phương khi:
\(\dfrac{m}{4}=\dfrac{1}{-2}\Rightarrow m=-2\)
Cho các vectơ a → = 4 ; - 2 , b → = - 1 ; - 1 , c → = 2 ; 5 . Phân tích vecto b → theo hai vectơ a → và c → ta được:
![]()
![]()
![]()
![]()
Cho tam giác đều ABC . Gọi M,N ,P lần lượt là các điểm thoả mãn vectơ BM = k vectơ BC , 4 vectơ AN = 3 vectơ AB , 3 vectơ AP = 2 vectơ AC . a, Biểu diễn vectơ AM theo hai vectơ AB , AC . b, Tìm k để hai đường thẳng AM , NP vuông góc với nhau.
a) Ta có:
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)
Cho hình thôi ABCD tâm I. Hãy cho biết số khẳng định đúng trong các khẳng định sau?
a. vectơ AB = vectơ BC
b. vectơ AB = vectơ DC
c. vectơ IA = vectơ IO
d. vectơ IB = vectơ IA
e. |vectơ AB| = |vectơ BC|
f. 2|vectơ IA| = |vectơ BD|
A. 3
B. 4
C. 5
D. 6
trong không gian cho 4 điểm A,B,C,D. Từ các điểm trên ta có thể lập được bao nhiêu vectơ khác vectơ không?
Cho lục giác đều ABCDEF có tâm O.
a) Tìm các vectơ khác vectơ O→ và cùng phương với vectơ OA→.
b) Tìm các vectơ bằng vectơ AB→.
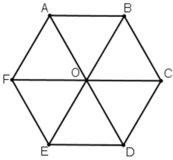
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
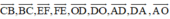
b) Các vectơ bằng vectơ AB→ là: