a/ Tìm tất cả giá trị của m để (-∞ ; m+1) ∩ [ 2m + 3; + ∞ ) = ∅
b/ Cho tập hợp A = {1;2;3;4;5;6} Tìm tất cả các tập con của tập A gồm ba phần tử sao cho tổng các phân tử này là một số chẵn
Những câu hỏi liên quan
1,Tìm tất cả các giá trị của m để hàm số y2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x2.
2, Tìm tất cả các giá trị của m để hàm số y x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x2.
3, Tìm tất cả các giá trị của m để hàm số yx^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu .
4, Tìm m để hso yx^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu.
Mọi người giúp em với ạ . Em cảm ơn ạ !
Đọc tiếp
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Câu 2: Cho các hàm số bậc nhất \(y=\left(m-2\right)x+2\)
a. Tìm tất cả các giá trị của m để hàm số đã cho đồng biến trên R
b. Tìm tất cả các giá trị của m để đồ thị hàm số đã cho song song với đường thẳng \(y=5x+1\)
a) Để đồ thị hàm số \(y=\left(m-2\right)x+2\) đồng biến trên R.
=> \(m-2>0.\)
<=> \(m>2.\)
b) Đồ thị hàm số \(y=\left(m-2\right)x+2\) song song với đường thẳng \(y=5x+1.\)
=> \(m-2=5.\)
<=> \(m=7.\)
Đúng 2
Bình luận (0)
Câu 2
a) Để hs đã cho đồng biến trên R thì:
\(m-2>0\\ < =>m>2\)
b) Đề đths đã cho song song với đường thẳng \(y=5x+1\) thì:
\(m-2=5\\ < =>m=7\)
Đúng 2
Bình luận (0)
Gọi A, B lần lượt là các giá trị nhỏ nhất, giá trị lớn nhất của hàm số 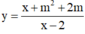trên đoạn [3;4]. Tìm tất cả các giá trị thực của tham số m để A+B
19
2
Đọc tiếp
Gọi A, B lần lượt là các giá trị nhỏ nhất, giá trị lớn nhất của hàm số 
trên đoạn [3;4]. Tìm tất cả các giá trị thực của tham số m để A+B=
19
2
Cho hai tập hợp A = [1;3] và B = [m; m+1]. Tìm tất cả giá trị của tham số m để B ⊂ A.
A. m = 1
B. 1 < m < 2
C. 1 ≤ m ≤ 2
D. m = 2
a) Tìm tất cả các giá trị của tham số m để gleft(xright)4mx^2-4left(m-1right)x+m-3 luôn luôn âm với mọi x thuộc Rb) Tìm tất cả các giá trị của tham số m để fleft(xright)x^2-2left(m+2right)x-2m^2+3m+4 không âm với mọi m thuộc Rc) Bất pt x^2+2mx+m^2-5m+60 ( m là tham số thực) có nghiệm với mọi x thuộc R khi minleft(-infty;dfrac{a}{b}right) với a,bin Z và dfrac{a}{b} là phân số tối giản. Tính giá trị biểu thức a+2b
Đọc tiếp
a) Tìm tất cả các giá trị của tham số m để \(g\left(x\right)=4mx^2-4\left(m-1\right)x+m-3\) luôn luôn âm với mọi x thuộc R
b) Tìm tất cả các giá trị của tham số m để \(f\left(x\right)=x^2-2\left(m+2\right)x-2m^2+3m+4\) không âm với mọi m thuộc R
c) Bất pt \(x^2+2mx+m^2-5m+6>0\) ( m là tham số thực) có nghiệm với mọi x thuộc R khi \(m\in\left(-\infty;\dfrac{a}{b}\right)\) với \(a,b\in Z\) và \(\dfrac{a}{b}\) là phân số tối giản. Tính giá trị biểu thức a+2b
cho (P):y=1/2x^2 và (d):y=x-m
a) tìm tất cả các giá trị của m để (d) cắt (P) tại 2 điểm phân biệt nằm về cùng nửa mặt phẳng bờ là trục tung
b) tìm tất cả các giá trị m thuộc(P) sao cho khoảng cách từ M đến trục tung là 2
a.
Phương trình hoành độ giao điểm: \(\dfrac{1}{2}x^2=x-m\Rightarrow x^2-2x+2m=0\)
\(\Delta'=1-2m>0\Leftrightarrow m< \dfrac{1}{2}\) (do (d) cắt (P) tại 2 điểm phân biệt)
Để 2 điểm nằm cùng về phía trục tung thì 2 nghiệm \(x_1,x_2\) cùng dấu.
Mà theo vi ét \(x_1+x_2=2\Rightarrow\) 2 nghiệm cùng dương.
\(\Rightarrow x_1+x_2=2m>0\Leftrightarrow m>0\)
Kết hợp điều kiện ta có \(0< m< \dfrac{1}{2}\)
b.
Từ M đến trục tung là 2 \(\Rightarrow\) \(\left|x\right|=2\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(M\in\left(P\right)\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y_1=\dfrac{1}{2}.2^2=2\\y_2=\dfrac{1}{2}.\left(-2\right)^2=2\end{matrix}\right.\)
\(\Rightarrow M_1\in\left(2;2\right)\) và \(M_2\in\left(-2;2\right)\)
Đúng 1
Bình luận (0)
Cho hai tập hợp A [m; m+1] và B [0;3). Tìm tất cả các giá trị thực của tham số m để A
∩
B
∅
A.
m
∈
(
−
∞
;
−
1
)
∪
(
3
;
+
∞
)
.
B.
m
∈
(
−
∞
;
−
1...
Đọc tiếp
Cho hai tập hợp A = [m; m+1] và B = [0;3). Tìm tất cả các giá trị thực của tham số m để A ∩ B = ∅
A. m ∈ ( − ∞ ; − 1 ) ∪ ( 3 ; + ∞ ) .
B. m ∈ ( − ∞ ; − 1 ] ∪ ( 3 ; + ∞ ) .
C. m ∈ ( − ∞ ; − 1 ) ∪ [ 3 ; + ∞ ) .
D. m ∈ ( − ∞ ; − 1 ] ∪ [ 3 ; + ∞ ) .
Cho hai tập hợp A = [ 1;3 ] và B = [ m; m+1], Tìm tất cả các giá trị của tham số m để \(B\subset A\)
Để B là con của A
\(\left\{{}\begin{matrix}m\ge1\\m+1\le3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m\le2\end{matrix}\right.\)
Vậy 1 ≤ m ≤ 2
Đúng 0
Bình luận (0)
Cho hai tập hợp A = (− ∞ ; m] và B = (2; + ∞ ). Tìm tất cả các giá trị thực của tham số m để A ∪ B = R.
A. m > 0
B. m ≥ 2
C. m ≥ 0
D. m > 2
Cho hai tập hợp A (m−1;5) và B (3;+
∞
). Tìm tất cả các giá trị thực của tham số m để A∖B
∅
A.
m
≥
4
.
B. m 4 C.
4
≤
m
6
.
D.
4
≤
m
≤
6
.
Đọc tiếp
Cho hai tập hợp A = (m−1;5) và B = (3;+ ∞ ). Tìm tất cả các giá trị thực của tham số m để A∖B = ∅
A. m ≥ 4 .
B. m = 4
C. 4 ≤ m < 6 .
D. 4 ≤ m ≤ 6 .
