Cho \(\Delta\) ABC vuông ở A, AB = 6, AC = 8; đường cao AH, phân giác BD. Gọi I là giao điểm của AH và BD.
a, Tính AD, DC
b, Chứng minh \(\frac{IH}{IA}=\frac{AD}{DC}\)
c, Chứng minh AB . BI = BD . HB và \(\Delta\) AID cân
TAM GIÁC ĐỒNG DẠNG
1, a) Cho AB=6 dm, AC=15 cm , tìm tỉ số hai đoạn thẳng AB và AC .
b) Cho AB=6 cm, AC=18 cm , tìm tỉ số hai đoạn thẳng AB và AC .
2, ΔMNP _____ ΔABC thì : a) \(\frac{MN}{AB}=\)........ b) \(\frac{MP}{AC}=........\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
b) Cho \(\Delta ABC\) có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
5. a) Cho \(\Delta DEF\sim\Delta ABC\) theo tỉ số đồng dạng k = 2. Tìm tỉ số \(\frac{S_{DÈF}}{S_{ABC}}\)
b) Cho \(\Delta DEF\)\(\sim\Delta ABC\) theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số \(\frac{S_{DEF}}{S_{ABC}}\)
6. Cho \(\Delta ABC.\)Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho \(\frac{AD}{AB}=\frac{AE}{AC}.\)Kết luận nào sai ❓
A. \(\Delta ADE\sim\Delta ABC\) B. DE//BC C. \(\frac{AE}{AD}=\frac{AC}{AB}\) D. \(\Delta ADE=\Delta ABC\)
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.\(\Delta ABC\sim\Delta DEF\) B. \(\Delta ABC\sim\Delta EDF\)
C. \(\Delta ABC\sim\Delta DFE\) D.\(\Delta ABC\sim\Delta FED\)
giải giúp mình với! Mình cần gấp
TAM GIÁC ĐỒNG DẠNG
1, a) Tỉ số hai đoạn thẳng AB và AC : \(\frac{AB}{AC}=\frac{6}{15}\)
b) Tỉ số hai đoạn thẳng AB và AC . : \(\frac{AB}{AC}=\frac{6}{18}=\frac{1}{3}\)
2, ΔMNP ~ ΔABC thì : \(\frac{MN}{AB}=\frac{NP}{BC}=\frac{MP}{AC}\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
Bạn ơi D ở đâu vậy ?
b) Cho ΔABCΔABC có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
Xét \(\Delta ABC\) có AD là phân giác
\(\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\Rightarrow BD=\frac{AB.CD}{AC}=3cm\)
5. a) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k = 2. Tìm tỉ số SDÈFvà SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=2^2=4\)
b) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số SDEF và SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
6. Cho ΔABC..Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho AD/AB=AE/AC Kết luận nào sai ❓
A. ΔADE∼ΔABC B. DE//BC
C. AE/AD=AC/AB D. ΔADE=ΔABC
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.ΔABC∼ΔDEF B. ΔABC∼ΔEDF
C. ΔABC∼ΔDFE D.ΔABC∼ΔFED
Cho tứ diện ABCD có \(\Delta\)ABC vuông tại A, AB=6 , AC=8. \(\Delta\)BCD có độ dài đường cao kẻ từ đỉnh C bằng 8. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABC). Tính góc giữa mặt phẳng (ABD) và (BCD) .
1. Cho ΔABC vuông tại A; AB=6, AC=8; đường p/g AD.
a, Tính độ dài cạnh DA; DC b, Tia p/g ∠C cắt AD tại I. Gọi M là trung điểm của BC. C/m ∠BIM = 90o
2.Cho ΔABC nhọn, H là trực tâm . gọi M là trung diểm của BC. Đường thẳng qua H ⊥ MH cắt AB, AC tại I, K.
C/m : a. ΔAIH ∼ ΔCHM ; ΔAKH∼ ΔBHM b. HI = HK
3. Gọi AD là đường cao, H là trực tâm của ΔABC nhọn, có BC=a không đổi.
a. C/m ΔADB∼ ΔCDH b.Tính GTLL của DA.DH
4. Cho ΔABC vuông tại A, AB=36 cm, AC=48cm; đường p/g AK ; tia p/g ∠B cắt AK tại I. Qua I kẻ đường thẳng // BC cắt AB , AC tại D , E.
a. Tính độ dài cạnh BK b.Tính tỉ số \(\dfrac{AD}{AB}\) c. Tính độ dài cạnh DE
1. Cho Tam giác ABC có cạnh AB<AC. Đường cao AH, Phân giác Góc HAC cắt BC tại D. DK vuông AC tại K
a. CM tam giác AHD = AKD
b. Cm AD vuông HK
c. có AH=6 cm, HC=8 cm. Tinh AC
D. QUA C kẻ đoạn thẳng vuông AD, cắt tia KD ở I.CM A,H,I thẳng hàng
Cho ΔABC vuông tại A, BI là đường phân giác (I ∈ AC). kẻ CH ⊥ đường thẳng BI (H ∈ BI)
a, chứng minh: ΔABI∼ΔHCL.
b, Chứng minh: góc IBC = góc ICH
c,Cho biêta AB=6 cm; AC=8 cm. Tính độ dài cạnh AI,IC
d, Tính tỉ số diện tích của ΔABI và ΔHBC
a) Xét ΔABI và ΔHCI có
\(\widehat{BAI}=\widehat{CHI}\left(=90^0\right)\)
\(\widehat{AIB}=\widehat{HIC}\)(hai góc đối đỉnh)
Do đó: ΔABI∼ΔHCI(g-g)
b) Ta có: ΔABI∼ΔHCI(cmt)
⇒\(\widehat{ABI}=\widehat{HCI}\)(hai góc tương ứng)
mà \(\widehat{ABI}=\widehat{IBC}\)(BI phân giác)
nên \(\widehat{IBC}=\widehat{ICH}\)(đpcm)
c) Áp dụng định lí pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay \(BC=\sqrt{100}=10cm\)
Xét ΔBAC có BI là đường phân giác ứng với cạnh AC(gt)
nên \(\frac{AI}{BA}=\frac{CI}{BC}\)(tính chất đường phân giác của tam giác)
hay \(\frac{AI}{6}=\frac{CI}{10}\)
Ta có: AI+CI=AC(I nằm giữa A và C)
hay AI+CI=8cm
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{AI}{6}=\frac{CI}{10}=\frac{AI+CI}{6+10}=\frac{8}{16}=\frac{1}{2}\)
Do đó: \(\left\{{}\begin{matrix}\frac{AI}{6}=\frac{1}{2}\\\frac{CI}{10}=\frac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AI=\frac{6}{2}=3cm\\CI=\frac{10}{2}=5cm\end{matrix}\right.\)
Vậy: AI=3cm;CI=5cm
Cho tam giác ABC vuông ở A , có AB = 6 cm , AC = 8 cm . Độ dài cạnh BC là:
A. 9 cm B. 10 cm C. 11 cm D.12cm
Áp dụng định lý pytago cho tam giác `ABC` ta có :
`BC^2= AB^2+AC^2`
`BC^2=6^2+8^2`
`BC^2= 36+64`
`BC^2=100`
`=>BC=10(cm)`
`->B`
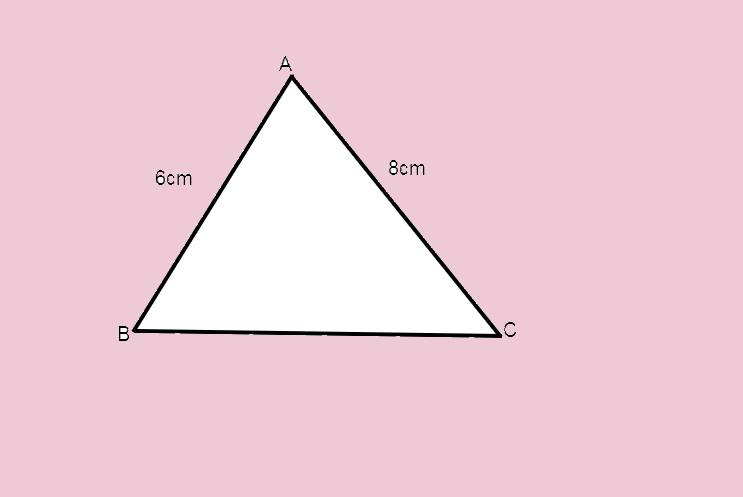
Cho tam ABC vuông tại A có AB=6, AC=8. a, tính độ dài cạnh BC. b, đương qhan giác góc B cắt AC tại D vẽ DH vuông góc BC (H thuộc BC. Cm tam giác ABD=HBD. c, CM DA<D
(Tự vẽ hình)
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
b) Xét \(\Delta ABD\) và \(\Delta HBD\) có:
\(\widehat{BAD}=\widehat{BHD}=90^0\)
\(BD\) chung
\(\widehat{ABD}=\widehat{HBD}\) (tính chất phân giác)
\(\Rightarrow\Delta ABD=\Delta HBD\) (ch - gn)
c) Ta có \(\Delta ABD=\Delta HBD\Rightarrow AD=HD\)
Mà \(HD< DC\) (do \(\Delta HDC\) vuông tại \(H\))
\(\Rightarrow DA< DC\)
a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AC^2+AB^2}=10cm\)
b, Xét tam giác BAD và tam giác BHD có
BD _ chung ; ^ABD = ^HBD ; ^BAD = ^BHD = 900
Vậy tam giác BAD = tam giác BHD ( ch-gn)
Cho△ABC vuông ở A , có AB = 6 cm , AC = 8 cm . Vẽ đường cao AH ( H thuộc BC )
a/ Tính diện tích △vuông ABC
b/ Vẽ phân giác AD của góc A ( D thuộc BC ) . Tính DB , DC c / Chứng minh :
α)△ABC và△HBA đồng dạng
β) AB² = BH.BC
γ)1/AH²=1/AB²+1/AC²
Cho tam giác ABC vuông ở A, AC=6, $\hat{C}=30^0$. Vẽ (O) đường kính AC cắt BC tại D, dây DE vuông góc AC tại H. Qua B vẽ tiếp tuyến của (O) tại M.
a. Tính BC và chứng minh tam giác CDE đều.
b. Chứng minh: $\Delta BDM$ ~ $\Delta BMC$.
c. Gọi K là hình chiếu của H trên EC và I là trung điểm HK. Chứng minh: DK vuông góc CI.
cho \(\Delta\)ABC có AB<AC vuông tại B, phân giác AD của góc A cắt BC tại D. từ D kẻ DH vuông góc với AC (H∈AC);và HD và AB kéo dài cắt tai I. Chứng minh rằng:
a) \(\Delta\)ABC = \(\Delta\)AHD
b) AD là trung trực của BH
c) \(\Delta\)DIC cân
d)BH//IC
e) AD\(\perp\)IC
g) BC > AD + AD - 2AB
a: Xet ΔABD vuông tại B và ΔAHD vuông tại H có
AD chung
góc BAD=góc HAD
=>ΔABD=ΔAHD
b; AB=AH
DB=DH
=>AD là trung trực của BH
c: Xet ΔDBI vuông tại B và ΔDHC vuông tại H có
DB=DH
góc BDI=góc HDC
=>ΔBDI=ΔHDC
=>DI=DC
=>ΔDIC cân tại D
d: Xét ΔAIC có AB/BI=AH/HC
nên BH//IC
e: AD vuông góc BH
BH//IC
=>AD vuông góc IC