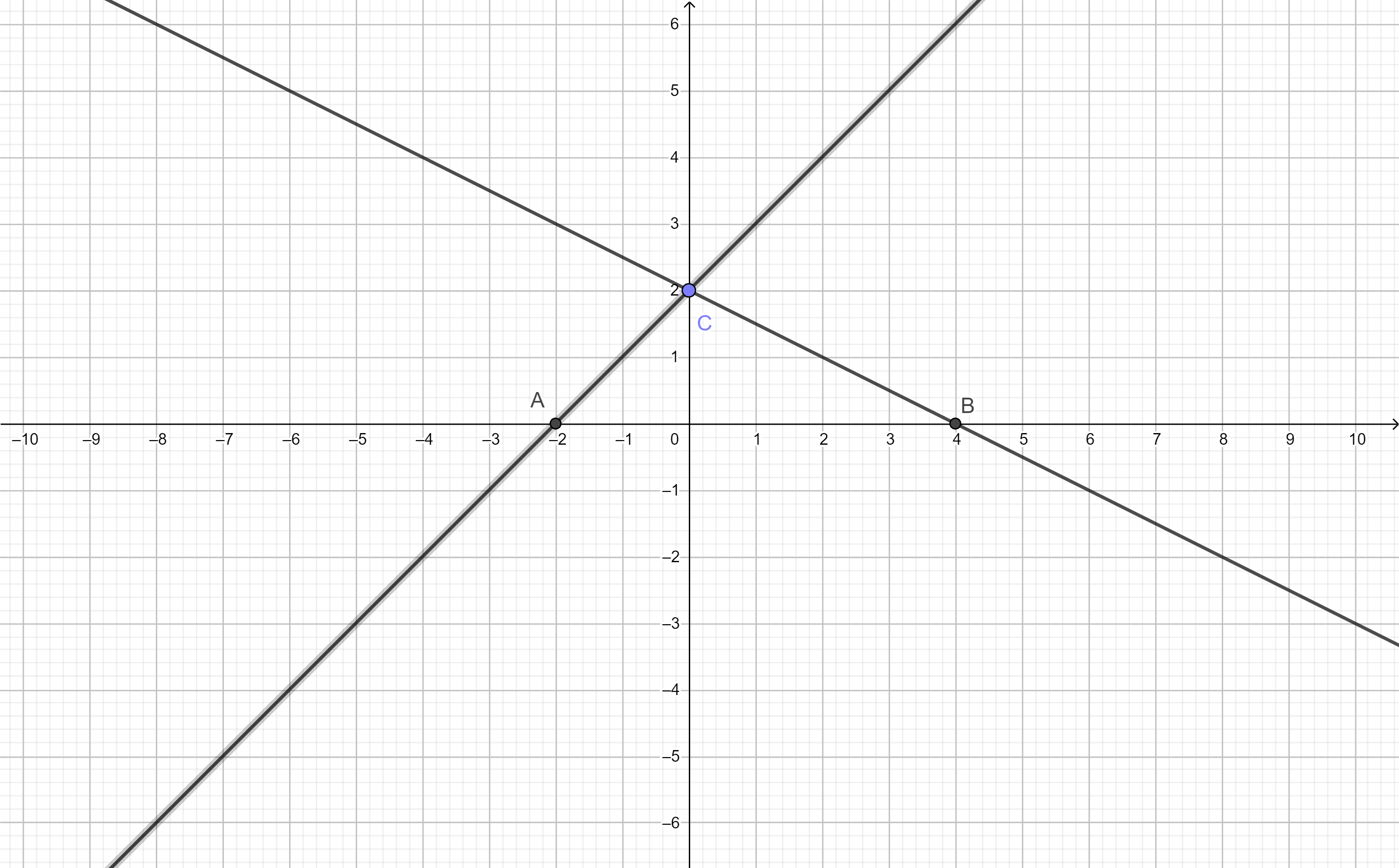
Gọi giao điểm của hai đường thẳng
y
=
1
2
x
+
2
;
y
=
-
x
+
2
với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tính các góc của tam giác ABC (làm tròn đến độ)