tìm số tự nhiên n để đa thức D chia hết cho đa thức E
D=2011xn-1y6-2011xn+1y4 ; E=2011x3yn
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B:
a) A = - 13 x 17 y 2 n - 3 + 22 x 16 y 7 ; B = - 7 x 3 n + 1 y 6 ;
b) A = 20 x 5 y 2 n - 10 x 4 y 3 n + 15 x 5 y 6 ; B = 3 x 2 y n + 1 .
Tìm điều kiện của số tự nhiên n (n > 0) để đơn thức B = 4 x 4 y 4 chia hết đơn thức C = x n - 1 y 4 là
A. n = 5
B. 0 < n ≤ 5
C. n ≥ 5
D. n = 0
Ta có B : C = ( 4 x 4 y 4 ) : ( x n - 1 y 4 )
Đơn thức B chia hết cho đơn thức C khi 4 ≥ n – 1 => n ≤ 5
Hay 0 < n ≤ 5
Đáp án cần chọn là: B
Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Vì \(A\left(x\right)=x^{2n}+x^n+1\) chỉ có một hằng số là1
đa thức \(x^2+x+1\) cũng chỉ có một hằng số là 1
Để \(A\left(x\right)⋮x^2+x+1\) thì thì \(A\left(x\right)\) phải có số mũ tương ứng với các bậc như đa thức : => n=1
-Đáp án cuối cùng: \(n=3k+1\) hay \(n=3k+2\)



Tìm số tự nhiên n để đa thức:
A(x)=x2n+xn+1 chia hết cho đa thức x2+x+1.
Tìm số tự nhiên n để đa thức A chia hết cho đa thức B khi A=x^2.y^4 +2x^3.y^3 và B=x^n.y^3
Ta có: \(A=x^2y^4+2x^3y^3\)
Để A chia hết cho \(B=x^ny^3\) thì:
\(\left\{{}\begin{matrix}2x^3y^3⋮x^ny^3\\x^2y^4⋮x^ny^3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^3⋮x^n\\x^2⋮x^n\end{matrix}\right.\)
\(\Rightarrow x^0\le x^n\le x^2\)
\(\Rightarrow0\le n\le2\)
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7 x n - 1 y 5 - 5 x 3 y 4 ; B = 5 x 2 y n
Ta có
A : B = ( 7 x n - 1 y 5 - 5 x 3 y 4 ) : ( 5 x 2 y n ) = 7 / 5 x n - 3 y 5 - 5 - x y 4 - n
Theo đề bài đa thức A chia hết cho đơn thức B
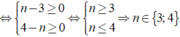
Vậy giá trị n cần tìm là n∈{3; 4}
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7 x n - 1 y 5 - 5 x 3 y 4 ;
B = 5 x 2 y n
Bài 5. (0,5 điểm) Cho đa thức A = và đơn thức B = . Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B.
Để A ⋮ B thì:
3n ≤ 9 và 2n ≥ 4
n ≤ 3 và n ≥ 2
n = 2 hoặc n = 3