Cho hai đường thẳng (d1): y = 12x + 5 - m; (d2): y = 3x + 3 + m. Xác định m để giao điểm của (d1) và (d2) thỏa mãn nằm trên trục tung.

Những câu hỏi liên quan
Cho hàm số
y
m
x
–
2
có đồ thị là đường thẳng
d
1
và cắt hàm số
y
1
2
x
+
1
có đồ thị là đường thẳng
d
2
. Xác định m để hai đường thẳng
d
1
v
à
d
2
cắt nhau tại một điểm có hoành đ...
Đọc tiếp
Cho hàm số y = m x – 2 có đồ thị là đường thẳng d 1 và cắt hàm số y = 1 2 x + 1 có đồ thị là đường thẳng d 2 . Xác định m để hai đường thẳng d 1 v à d 2 cắt nhau tại một điểm có hoành độ x = − 4
A. m = − 1 4
B. m = 1 4
C. m = 1 2
D. m = - 1 2
Ta có phương trình hoành độ giao điểm của d 1 v à d 2 : m x – 2 = 1 2 x + 1 ( * )
Để hai đường thẳng d 1 v à d 2 cắt nhau tại một điểm có hoành độ x = − 4 t h ì x = − 4 thỏa mãn phương trình (*)
Suy ra m . ( − 4 ) – 2 = 1 2 . ( − 4 ) + 1 ⇔ − 4 m – 2 = − 2 + 1 ⇔ − 4 m = 1 ⇔ m = 1 4
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho hai đường thẳng:y (m + 1)x + 5
(
d
1
)
y 2x + n
(
d
2
)
Với giá trị nào của m và n thì:a)
d
1
trùng với
d
2
?b)
d
1
cắt
d
2
?c)
d
1
song song với
d
2
?
Đọc tiếp
Cho hai đường thẳng:
y = (m + 1)x + 5 ( d 1 )
y = 2x + n ( d 2 )
Với giá trị nào của m và n thì:
a) d 1 trùng với d 2 ?
b) d 1 cắt d 2 ?
c) d 1 song song với d 2 ?
a) Để d1 trùng d2 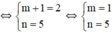
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 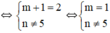
Vậy m = 1, n ≠ 5.
Đúng 0
Bình luận (0)
Cho hai đường thẳng:
y = (m + 1)x + 5 (d1)
y = 2x + n (d2)
Với giá trị nào của m và n thì:
a) d1 trùng với d2?
b) d1 cắt d2?
c) d1 song song với d2?
a) Để d1 trùng d2 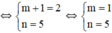
Vậy m = 1, n = 5
b) Để d1 cắt d2 thì: m + 1 ≠ 2 ⇒ m ≠ 1
c) Để d1 song song d2 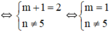
Vậy m = 1, n ≠ 5.
Đúng 0
Bình luận (0)
Cho đường thẳng (d1): y = kx + 5. Tìm k để đường thẳng (d1) song song với đường thẳng (d2) biết rằng (d2) đi qua hai điểm A(1 ; 2) và B(-3 ; -2).
Gọi pt d2 có dạng \(y=ax+b\)
Do d2 qua A và B nên ta có:
\(\left\{{}\begin{matrix}a+b=2\\-3a+b=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\) \(\Rightarrow d_2:y=x+1\)
Do \(d_1\) song song \(d_2\) nên chúng có cùng hệ số góc
\(\Rightarrow k=1\)
Đúng 0
Bình luận (0)
Cho đường thẳng
d
1
:
y
1
2
x
+
2
. Đường thẳng
d
2
đi qua A(2;4) và song song với có phương trình là: A.
y
-
1
2
x
+
2
B.
y
-
1
2
x
+
4...
Đọc tiếp
Cho đường thẳng d 1 : y = 1 2 x + 2 . Đường thẳng d 2 đi qua A(2;4) và song song với có phương trình là:
A. y = - 1 2 x + 2
B. y = - 1 2 x + 4
C. y = 1 2 x + 3
D. y = 1 2 x + 4
Do đường thẳng d2 song song với d1 nên d2 có dạng : y = 1 2 x + b b ≠ - 2
Điểm A(2; 4) thuộc đường thẳng d2 nên: 4 = 1 2 . 2 + b ⇔ b = 3
Vậy phương trình đường thẳng d2: y = 1 2 x + 3
Chọn đáp án là C.
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y=2mx + m - 1 có đồ thị (d1). Tìm m để:
a) Đường thẳng (d1) song song với đường thẳng y= -\(\dfrac{1}{3}\)x + 1
b) (d1) trùng với đường thẳng -2x - y = 5
a.
Để hai đường thẳng song song:
\(\Rightarrow\left\{{}\begin{matrix}2m=-\dfrac{1}{3}\\m-1\ne1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-\dfrac{1}{6}\\m\ne2\end{matrix}\right.\) \(\Leftrightarrow m=-\dfrac{1}{6}\)
b.
\(-2x-y=5\Leftrightarrow y=-2x-5\)
Để hai đường thẳng trùng nhau:
\(\Leftrightarrow\left\{{}\begin{matrix}2m=-2\\m-1=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=-1\\m=-4\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
Vậy ko tồn tại m để 2 đường thẳng trùng nhau
Đúng 1
Bình luận (1)
a, A = b, 2, Cho hai đường thẳng (d1): y = (2m-5).x – m – 2 và (d2): y = - 3 – x. Tìm m để hai đường thẳng cắt nhau tại một điểm nằm trên trục tung.
PTHDGD: \(\left(2m-5\right)x-m-2=-3-x\)
2 đt cắt tại 1 điểm trên trục tung nên x=0
\(\Leftrightarrow-m-2=-3\Leftrightarrow m=1\)
Đúng 0
Bình luận (0)
Cho đường thẳng (d1): y=(m-1)x+m-2 và đường thẳng (d2): y=-2x+3. Tìm giá trị của m để hai đoạn thẳng (d1) và (d2) song song với nhau
Để (d1 ) và (d2 ) song song thì
+) b≠b'
⇔m-2≠3
⇔m≠5
+) a=a'
⇔m-1=-2
⇔m=-1 (thỏa mãn điều kiện)
Vậy tại m=-1 thì (d1) // (d2)
Đúng 0
Bình luận (0)
Cho hai đường thẳng x + y = -1 (d1) và mx + y = 1 (d2). Tìm m để hai đường thẳng (d1) và (d2) cắt nhau tại một điểm thuộc trục hoành
Lời giải:
Giao điểm của 2 đường thẳng thuộc trục hoành nên có dạng $(a,0)$. Vì điểm này thuộc $(d_1):x+y=-1$ nên $a+0=-1\Rightarrow a=-1$
Vậy giao điểm của 2 ĐT trên là $(-1,0)$
Giao điểm này $\in (d_2)$ khi mà $m.(-1)+0=1$
$\Leftrightarrow m=-1$
Đúng 0
Bình luận (0)
Cho 2 đường thẳng: y= -3x -7 (d1) và y=2x+3 (d2)
Tìm tọa độ giao điểm M của hai đường thẳng (d1) , (d2)
Gọi \(A\left(x_0;y_0\right)\) là giao điểm \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}y_0=-3x_0-7\\y_0=2x_0+3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_0=-\dfrac{4}{5}\\y_0=-\dfrac{23}{5}\end{matrix}\right.\)
\(\Rightarrow M\left(-\dfrac{4}{5};-\dfrac{23}{5}\right)\)
Đúng 1
Bình luận (0)
















