cho hpt:
x - 2y = 1 + 3m
2x + y = m + 2
Tìm giá trị của m để x2 - y2 có giá trị nhỏ nhất. Biết (x ; y) là nghiệm của hệ phương trình trên!!!
Cho hpt:
x+my=m+1 (1)
mx+y=3m-1(2)
a, giải hpt khi m=2
b, tìm m để hệ có nghiệm duy nhất (x,y) sao cho x.y có giá trị nhỏ nhất
a) Thay m=2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+2y=3\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=6\\2x+y=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3x=1\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\2y=3-x=3-\dfrac{1}{3}=\dfrac{8}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: Khi m=2 thì hệ phương trình có nghiệm duy nhất là \(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{4}{3}\end{matrix}\right.\)
Cho x, y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y Tính giá trị M + m
A. 41
B. 44
C. 42
D. 43
Cho x , y là các số thực thỏa mãn x + y = x - 1 + 2 y + 2 . Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 2 + y 2 + 2 ( x + 1 ) ( y + 1 ) + 8 4 - x - y . Khi đó, giá trị của M+m bằng.
A. 41
B. 42
C. 43
D. 44
2) Cho A= x2-2xy+y2-2y+2003
Với giá trị nào của x,y thì A có giá trị nhỏ nhất. Tìm giá trị đó
Cho hệ phương trình \(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\) (với m là tham số)
Tìm m để hệ đã cho có nghiệm (x;y) thỏa mãn: x2 + y2 + 3 đạt giá trị nhỏ nhất.
\(\left\{{}\begin{matrix}3x-y=2m-1\\x+2y=3m+2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}6x-2y=4m-2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x-2y+x+2y=4m-2+3m+2\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\x+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\m+2y=3m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\2y=2m+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=m+1\end{matrix}\right.\)
\(x^2+y^2+3\\ =m^2+\left(m+1\right)^2+3\\ =m^2+m^2+2m+1+3\\ =2m^2+2m+4\\ =2\left(m^2+m+2\right)\)
\(=2\left(m^2+m+\dfrac{1}{4}+\dfrac{7}{4}\right)\)
\(=2\left[\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\right]\)
\(=2\left(m+\dfrac{1}{2}\right)^2+\dfrac{7}{2}\ge\dfrac{7}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy ...
cho X, y>=0 sao cho X2+ Y2=1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của A= √2X+1+√2Y+1
với x;y>=0 ta có:
\(A^2=\left(\sqrt{2x+1}+\sqrt{2y+1}\right)^2=2x+1+2y+1+2\sqrt{\left(2x+1\right)\left(2y+1\right)}\)
\(=2\left(x+y\right)+2+\sqrt{4xy+2x+2y+1}=2\left(x+y\right)+2+\sqrt{4xy+2\left(x+y\right)+1}\)
\(2=2\left(x^2+y^2\right)=\left(1+1\right)\left(x^2+y^2\right)>=\left(x+y\right)^2\Rightarrow x+y< =\sqrt{2}\)(bđt bunhiacopxki)
\(2xy< =x^2+y^2=1\Rightarrow2\cdot2xy=4xy< =2\cdot1=2\)
\(\Rightarrow A^2=2\left(x+y\right)+2+2\sqrt{4xy+2\left(x+y\right)+1}< =2\sqrt{2}+2+2\sqrt{2+2\sqrt{2}+1}\)
\(=2\sqrt{2}+2+2\sqrt{\left(\sqrt{2}+1\right)^2}=2\sqrt{2}+2+2\left(\sqrt{2}+1\right)4\sqrt{2}+4\)
\(\Rightarrow A< =\sqrt{4\sqrt{2}+4}\)
dấu = xảy ra khi x=y=\(\sqrt{\frac{1}{2}}\)
vậy max A là \(\sqrt{4\sqrt{2}+4}\)khi \(x=y=\sqrt{\frac{1}{2}}\)
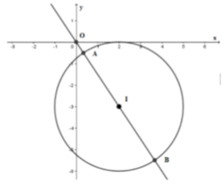
Cho hai số thực x, y thỏa mãn x 2 + y 2 - 4 x + 6 y + 4 + y 2 + 6 y + 10 = 6 + 4 x - x 2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T = x 2 + y 2 - a . Có bao nhiêu giá trị nguyên thuộc đoạn [-10;10] của tham số a để M ≥ 2 m
A. 17
B. 16
C. 15
D. 18
Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
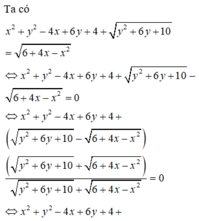
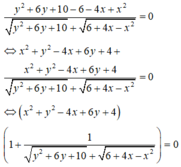


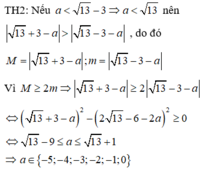

Xét các số thực x, y thỏa mãn
√x2+y2+4x−2y+5+√x2+y2−8x−14y+65=6√2
Gọi m và M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức T=x2+y2−2x+2y+2.Tính P = m + M
Bạn tham khảo nhé!
Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath

Cho hệ phương trình \(\left\{{}\begin{matrix}2x+y=3m-5\\x-y=2\end{matrix}\right.\)(m là tham số)
a, giải hệ phương trình với m=2
b, gọi nghiệm của hệ là (x;y), tìm giá trị của m để x2+y2 đạt giá trị nhỏ nhất
a, Thay m = 2 ta được \(\left\{{}\begin{matrix}2x+y=1\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
b, \(\Leftrightarrow\left\{{}\begin{matrix}3x=3m-3\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m-1\\y=m-3\end{matrix}\right.\)
Ta có : \(x^2+y^2=m^2-2m+1+m^2-6m+9=2m^2-8m+10\)
\(=2\left(m^2-4m+4-4\right)+10=2\left(m-2\right)^2+2\ge2\forall m\)
Dấu''='' xảy ra khi m =2
Vậy ...
Cho hàm số y = x 2 − 2(m + 1 m )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là y 1 , y 2 thỏa mãn y 1 - y 2 = 8. Khi đó giá trị của m bằng
A. m = 1
B. m ∈ ∅
C. m = 2
D. m = 1, m = 2