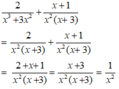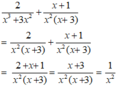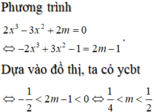2x3 cộng 3x2 trừ 32x bằng 48

Những câu hỏi liên quan
tìm x
x4-2x3+10x2-20x =0
x3-3x2-16x + 48=0
a: =>x^3(x-2)+10x(x-2)=0
=>(x-2)(x^3+10x)=0
=>x(x-2)(x^2+10)=0
=>x(x-2)=0
=>x=0 hoặc x=2
b: =>x^2*(x-3)-16(x-3)=0
=>(x-3)(x^2-16)=0
=>(x-3)(x+4)(x-4)=0
=>\(x\in\left\{3;4;-4\right\}\)
Đúng 1
Bình luận (0)
Làm tính cộng:
2
x
3
+
3
x
2
+
x
+
1
x
2
(
x
+
3
)
. A.
1
x
+...
Đọc tiếp
Làm tính cộng: 2 x 3 + 3 x 2 + x + 1 x 2 ( x + 3 ) .
A. 1 x + 3
B. 1 x 2
C. 1 x 2 x + 3
D. Đáp án khác
Kết quả của phép cộng
2
x
3
+
3
x
2
+
x
+
1
x
2
(
x
+
3
)
. A.
1
x...
Đọc tiếp
Kết quả của phép cộng 2 x 3 + 3 x 2 + x + 1 x 2 ( x + 3 ) .
A. 1 x + 3
B. 1 x 2
C. 1 x 2 x + 3
D. Đáp án khác
1) (1-x)(5x+3)=(3x-7)(x-1)
2) (x-2)(x+1)=x2-4
3) 2x3+3x2-32x=48
4) x2+2x-15=0
5) 2x(2x-3)=(3-2x)(2-5x)
6) x3-5x2+6x=0
7) (x2-5)(x+3)=0
8) (x+7)(3x-1)=49-x2
\(\left(1-x\right)\left(5x+3\right)=\left(3x-7\right)\left(x-1\right)\)
\(< =>\left(1-x\right)\left(5x+3+3x-7\right)=0\)
\(< =>\left(1-x\right)\left(8x-4\right)=0\)
\(< =>\orbr{\begin{cases}1-x=0\\8x-4=0\end{cases}< =>\orbr{\begin{cases}x=1\\x=\frac{1}{2}\end{cases}}}\)
\(\left(x-2\right)\left(x+1\right)=x^2-4\)
\(< =>\left(x-2\right)\left(x+1\right)=\left(x-2\right)\left(x+2\right)\)
\(< =>\left(x-2\right)\left(x+1-x-2\right)=0\)
\(< =>-1\left(x-2\right)=0\)
\(< =>2-x=0< =>x=2\)
\(2x^3+3x^2-32x=48\)
\(< =>x^2\left(2x+3\right)-16\left(2x+3\right)=0\)
\(< =>\left(x^2-16\right)\left(2x+3\right)=0\)
\(< =>\left(x-4\right)\left(x+4\right)\left(2x+3\right)=0\)
\(< =>\hept{\begin{cases}x=4\\x=-4\\x=-\frac{3}{2}\end{cases}}\)
Xem thêm câu trả lời
Chọn đa thức mà em cho là kết quả đúng:
(2x3 – 2x + 1) – (3x2 + 4x – 1) ?
2x3 + 3x2 – 6x + 2
2x3 – 3x2 – 6x + 2
2x3 – 3x2 + 6x + 2
2x3 – 3x2 – 6x – 2
Đọc tiếp
Chọn đa thức mà em cho là kết quả đúng:
| (2x3 – 2x + 1) – (3x2 + 4x – 1) = ? | 2x3 + 3x2 – 6x + 2 |
| 2x3 – 3x2 – 6x + 2 | |
| 2x3 – 3x2 + 6x + 2 | |
| 2x3 – 3x2 – 6x – 2 |
Đặt và thực hiện phép tính ta có :
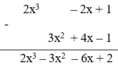
Vậy chọn đa thức thứ hai.
Đúng 0
Bình luận (0)
Rút gọn các phân thức sau1) 9 - ( x + 5)2 / x2 + 4x + 42) 32x - 8x2 + 2x3 / x3 + 643) 5x3 + 5x / x4 -14) 3x2 - 12x + 12 / x4 - 8x5) 2a2 - 2ab / ac + ad - bc -bd6) x2 - xy / y2 - x27) 2 - 2a / a3 - 18) x7 - x4 / x6 - 19) ( x + 2 )2 - ( x - 2)2 / 16x10) 24,5x2 - 0,5y2 / 3,5x2 - 0,5xy11) a3 - 3a2 + 2a - 6 / a2 +212) ( a - b) ( c - d) / (b2- a2) ( d2 - c2)Giúp mình với ạ, mình cảm ơn !
Đọc tiếp
Rút gọn các phân thức sau
1) 9 - ( x + 5)2 / x2 + 4x + 4
2) 32x - 8x2 + 2x3 / x3 + 64
3) 5x3 + 5x / x4 -1
4) 3x2 - 12x + 12 / x4 - 8x
5) 2a2 - 2ab / ac + ad - bc -bd
6) x2 - xy / y2 - x2
7) 2 - 2a / a3 - 1
8) x7 - x4 / x6 - 1
9) ( x + 2 )2 - ( x - 2)2 / 16x
10) 24,5x2 - 0,5y2 / 3,5x2 - 0,5xy
11) a3 - 3a2 + 2a - 6 / a2 +2
12) ( a - b) ( c - d) / (b2- a2) ( d2 - c2)
Giúp mình với ạ, mình cảm ơn !
1: \(=\dfrac{-\left[\left(x+5\right)^2-9\right]}{\left(x+2\right)^2}=\dfrac{-\left(x+5-3\right)\left(x+5+3\right)}{\left(x+2\right)^2}\)
\(=\dfrac{-\left(x+2\right)\left(x+8\right)}{\left(x+2\right)^2}=\dfrac{-\left(x+8\right)}{x+2}\)
2: \(=\dfrac{2x\left(x^2-4x+16\right)}{\left(x+4\right)\left(x^2-4x+16\right)}=\dfrac{2x}{x+4}\)
3: \(=\dfrac{5x\left(x^2+1\right)}{\left(x^2-1\right)\left(x^2+1\right)}=\dfrac{5x}{x^2-1}\)
4: \(=\dfrac{3\left(x^2-4x+4\right)}{x\left(x^3-8\right)}=\dfrac{3\left(x-2\right)^2}{x\left(x-2\right)\left(x^2+2x+4\right)}\)
\(=\dfrac{3\left(x-2\right)}{x\left(x^2+2x+4\right)}\)
5: \(=\dfrac{2a\left(a-b\right)}{a\left(c+d\right)-b\left(c+d\right)}=\dfrac{2a\left(a-b\right)}{\left(c+d\right)\left(a-b\right)}=\dfrac{2a}{c+d}\)
6: \(=\dfrac{x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}\cdot\left(-1\right)=\dfrac{-x}{x+y}\)
7: \(=\dfrac{2\left(1-a\right)}{-\left(1-a^3\right)}=\dfrac{-2\left(1-a\right)}{\left(1-a\right)\left(1+a+a^2\right)}=-\dfrac{2}{1+a+a^2}\)
8: \(=\dfrac{x^4\left(x^3-1\right)}{\left(x^3-1\right)\left(x^3+1\right)}=\dfrac{x^4}{x^3+1}\)
9: \(=\dfrac{\left(x+2-x+2\right)\left(x+2+x-2\right)}{16x}=\dfrac{4\cdot2x}{16x}=\dfrac{1}{2}\)
10: \(=\dfrac{0.5\left(49x^2-y^2\right)}{0.5x\left(7x-y\right)}=\dfrac{1}{x}\cdot\dfrac{\left(7x-y\right)\left(7x+y\right)}{7x-y}\)
\(=\dfrac{7x+y}{x}\)
Đúng 0
Bình luận (0)
Tìm bậc của mỗi đa thức sau
a) f (x) = 3x2 + 2x3 - 6x - 2
b) g(x) = 5x2 + 9 - 2x3 - 3x2 - 4x + 2x3 - 2
f (x) = 3x2 + 2x3 - 6x - 2
bậc của đa thức là: 3
g(x) = 5x2 + 9 - 2x3 - 3x2 - 4x + 2x3 - 2
g(x) = ( 5x2 - 3x2 ) + ( 9 -2) + ( - 2x3 + 2x3 ) - 4x
g(x) = 2x2 + 7 - 4x
bậc của đa thức là : 2
Đúng 3
Bình luận (0)
Cho hàm số
y
-
2
x
3
+
3
x
2
-
1
có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình
2
x
3
-
3
x
2
+
2
m
có đúng 3 nghiệm phân biệt, tron...
Đọc tiếp
Cho hàm số y = - 2 x 3 + 3 x 2 - 1 có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình 2 x 3 - 3 x 2 + 2 m có đúng 3 nghiệm phân biệt, trong đó có 2 nghiệm lớn hơn 1 2
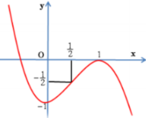
A. m ∈ - 1 2 ; 0
B. m ∈ - 1 ; 0
C. m ∈ 0 ; 1 2
D. m ∈ 1 4 ; 1 2
Câu 48/Đề 7: Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] đêể bất phương trình log3(x2+x+1)+2x3 ≤ 3x2 + log3x +m-1 có ít nhất 2 nghiệm phân biệt