Cho tam giác MNP cân tại M kẻ MI vuông góc NP ( I thuộc NP) chứng minh
a, ∆ MIN=∆MIP
b, IN=IP
Cho tam giác MNP cân tại M, MI là đường phân giác (I thuộc NP) a) chứng minh tam giác MIN=tam giác MIP b) kẻ EI vuông góc MN tại E , IF vuông góc MP tại F .chứng minh tam giác MEF cân
a)Ta có △MIP cân tại M nên \(\widehat{MNI}=\widehat{MPI}\)
Xét △MIN và △MIP có:
\(\widehat{NMI}=\widehat{PMI}\)
MI : cạnh chung
\(\widehat{MNI}=\widehat{MPI}\)
Nên △MIN = △MIP (c.g.c)
b)Gọi O là giao điểm của EF và MI
Vì △MNP là tam giác cân và MI là đường phân giác của △MIP
Suy ra MI đồng thời là đường cao của △MNP
Nên \(\widehat{MOE}=\widehat{MOF}=90^o\)
Xét △MOE vuông tại O và △MOF vuông tại O có:
OM : cạnh chung
\(\widehat{EMO}=\widehat{FMO}\)(vì MI là đường phân giác của △MIP và O\(\in\)MI)
Suy ra △MOE = △MOF (cạnh góc vuông – góc nhọn kề)
Nên ME = MF
Vậy △MEF cân
Cho tam giác MNP vuông tại N biết MN=6 , MP =10 . Kẻ MI là phân giác góc M ( I thuộc NP ) từ I kẻ IH vuông góc với MP ( H thuộc MP )
a) tính IN /IP
b) chứng minh MN.HI = MH.NP
c) tính diện tích tam giác MNI
a: IN/IP=MN/MP=3/5
c: NP=căn 10^2-6^2=8cm
NI là phân giác
=>NI/MN=IP/MP
=>NI/3=NP/5=8/8=1
=>NI=3cm
S MNI=1/2*3*6=9cm2
Cho tam giác MNP cân tại M có MN =MP 8cm , NP=10cm.
Kẻ MI vuông góc với NP (I thuộc NP)
a chứng minh rằng: IB =IC
b. Kẻ IH vuông góc với MN (H thuộc MN),IK vuông với MP (K thuộc MP). Chứng minh IH=IK
cho tam giác MNP cân tại M coa MN=MP=13cm, NP=10cm. kẻ MI vuông góc với NP (IϵNP)
A, chứng minh rằng: IN=IP
B,tính độ dài MI
C, kẻ IH vuông góc với MN (HϵMN), IK vuông góc với MP (KϵMP).chứng minh IH=IK
Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK
cho tam giác mnp vuông tại m trên np lấy e sao cho ne=nm qua e kẻ kẻ đường thẳng vuông góc với np cắt mp ở i chứng minh tam giác mni=tam giác eni,c/m tam giác ime cân, so sánh im và ip,kẻ đường cao mk của tam giác mnp c/m me là tia p/g cua góc kmp , kẻ ph vuông góc với ni tại h cắt nm kéo dài ở f c/m E,I,F thẳng hàng
Cho ∆MNP vuông tại M có MN< MP. Kẻ đường phân giác NI của góc MNP ( I thuộc MP) .kẻ IK vuông góc NP a. Chứng minh rằng ∆IMN=∆IKN b. chứng minh rằng MI < IP c. Gọi Q là giao điểm của IK và MN , đường thẳng NI cắt QP tại D. Chứng minh rằng ND vuông góc QP
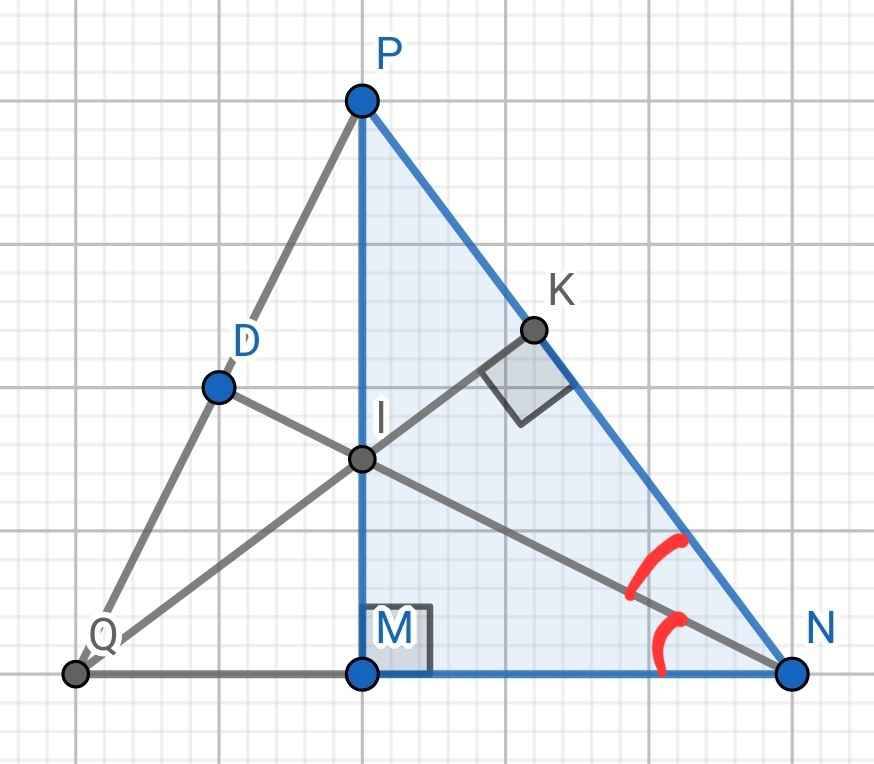
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
a) Xét ΔMNH vuông tại H và ΔMPH vuông tại H có
MN=MP(ΔMNP cân tại M)
MH chung
Do đó: ΔMHN=ΔMPH(cạnh huyền-cạnh góc vuông)
Suy ra: HN=HP(hai cạnh tương ứng)
b) Xét ΔINH vuông tại I và ΔEPH vuông tại E có
HN=HP(cmt)
\(\widehat{N}=\widehat{P}\)(Hai góc ở đáy của ΔMNP cân tại M)
Do đó: ΔINH=ΔEPH(cạnh huyền-góc nhọn)
Suy ra: HI=HE(Hai cạnh tương ứng)
Xét ΔHIE có HI=HE(cmt)
nên ΔHIE cân tại H(Định nghĩa tam giác cân)
Cho tam giác MNP cân tại M . MI là đường trung tuyến của tam giác MNP. kẻ NK vuông góc MP và cắt MI tại O.
chứng minh MI vuông góc np.
C/m PO vuông góc MN tại J.
C/m PK=NJ.
C/m Jk song song NP.
Kẻ phân giác góc MNO cắt MO tại H tính số đo góc MKH
Cho tam giác MNP cân tại Mc.Kẻ Nk vuông góc với MP ( k thuộc MP ).Kẻ PH vuông góc với MN ( h thuộc MN ).NK và PH cắt nhau tại I.
a.chứng minh rằng tam giác HNP=tam giác KPN.
b.so sánh góc HNI và góc KPI.
c.Đường thẳng MI cắt NP tại D,chứng minh rằng MD vuông góc với NP tại D
d.chứng minh rằng HK//NP