a/ Biểu diễn các điểm A(-1;-20;B(2;4) trên mặt phẳng tọa độ
b/ Viết công thức hàm số có ddoff thị là dduowfng thẳng đi qua hai điểm O và A
c/ Chứng tỏ các điểm A;B;O thẳng hàng
Những câu hỏi liên quan
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
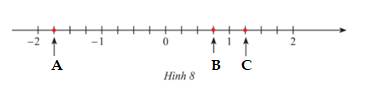
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:
Đúng 0
Bình luận (0)
a) Các điểm M, N, P trong Hình 6 biểu diễn các số hữu tỉ nào?
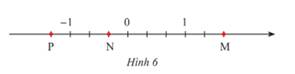
b) Biểu diễn các số hữu tỉ sau trên trục số: \( - 0,75;\,\frac{1}{{ - 4}};\,1\frac{1}{4}.\)
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)
Đúng 0
Bình luận (0)
Điểm P biểu diễn: \(-\dfrac{4}{3}\)
Điểm N biểu diễn: \(-\dfrac{1}{3}\)
Điểm M biểu diễn: \(\dfrac{5}{3}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Gọi A,B,C lần lượt là điểm biểu diễn hình học của các số phức z11-2i, z2-1+i và z33+4i. Điểm G trọng tâm tam giác ABC là điểm biểu diễn của số phức nào sau đây? A.z1-i. B.z3+3i. C.z1+2i. D.z1+i
Đọc tiếp
Gọi A,B,C lần lượt là điểm biểu diễn hình học của các số phức z1=1-2i, z2=-1+i và z3=3+4i. Điểm G trọng tâm tam giác ABC là điểm biểu diễn của số phức nào sau đây?
A.z=1-i.
B.z=3+3i.
C.z=1+2i.
D.z=1+i
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
;
z
2
2
+
i
;
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
−
i
;
z
2
2
+
i
;
z
3
−
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành. A.
z
−
3
−
i
B...
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = − i ; z 2 = 2 + i ; z 3 = − 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành.
A. z = − 3 − i
B. z = − 2 − i
C. z = − 3
D. z = - 1 − 3 i
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
,
z
2
2
+
i
,
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành A. z -3 - i B. z -2 – i C. z -1 –...
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i , z 2 = 2 + i , z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 – i
C. z = -1 – 3i
D. z = -3
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức
z
1
-
i
;
z
2
2
+
i
;
z
3
-
1
+
i
. Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành A. z -3 - i B. z -2 - i C. z -1 - 3i D. z -3
Đọc tiếp
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 - i
C. z = -1 - 3i
D. z = -3
Đáp án A
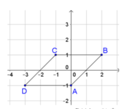
Ta có điểm A(0;-1), B(2;1), C(-1;1). Gọi D(a;b), khi đó ABCD là hình bình hành
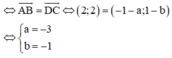
Suy ra số phức z biểu diễn D là z = -3 - i
Đúng 0
Bình luận (0)
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 1 + 2i; z2 -2 + 5i ; z3 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là A. -1 + 7i. B. 5 + i. C. 1 + 5i. D. 3 + 5i.
Đọc tiếp
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. -1 + 7i.
B. 5 + i.
C. 1 + 5i.
D. 3 + 5i.
Chọn B.
Ta có A(1 ;2) ; B(-2 ; 5),C(2 ;4).
Gọi D(x ; y).
Ta có 
Để ABCD là hình bình hành thì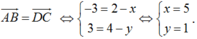 
Vậy z = 5 + i.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ, các điểm A, B, C theo thứ tự biểu diễn các số phức 2+3i, 3+i, 1+2i.Trọng tâm G của tam giác ABC biểu diễn số phức z. Tìm z
A. z=1+i
B.z=2+2i
C.z=2-2i
D.z=1-i
Biểu diễn các số nguyên: -3; -2; -1; 1; 2; 4 trên trục số rồi cho biết:a. Điểm biểu diễn số nguyên nào được đặt ở bên trái điểm 0, được đặt ở bên phải điểm 0. Từ đó rút ra nhận xét gì?b. Nhận xét gì về vị trí của các điểm -2 và điểm 2 đối với điểm 0?c. Nói rằng trên trục số điểm nào ở xa điểm 0 hơn thì biểu diễn số lớn hơn có đúng không?
Đọc tiếp
Biểu diễn các số nguyên: -3; -2; -1; 1; 2; 4 trên trục số rồi cho biết:
a. Điểm biểu diễn số nguyên nào được đặt ở bên trái điểm 0, được đặt ở bên phải điểm 0. Từ đó rút ra nhận xét gì?
b. Nhận xét gì về vị trí của các điểm -2 và điểm 2 đối với điểm 0?
c. Nói rằng trên trục số điểm nào ở xa điểm 0 hơn thì biểu diễn số lớn hơn có đúng không?
a. Điểm biểu diễn các số: - 2; - 3; - 1 đều đặt ở bên trái điểm 0 nên các số này đều nhỏ hơn số 0;
Điểm biểu diễn các số 1; 2; 4 đều đặt ở bên phải điểm 0 nên các số này đều lớn hơn số 0.
b. Điểm – 2 và 2 nằm về hai phía của điểm 0 và cách đều điểm 0.
c. Chỉ đúng với trường hợp những điểm nằm về bên phải điểm 0. Đối với những điểm nằm về bên trái điểm 0 thì ngược lại: điểm nào ở xa gốc hơn thì biểu diễn số nhỏ hơn.
Đúng 0
Bình luận (0)