Đáp án A
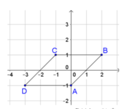
Ta có điểm A(0;-1), B(2;1), C(-1;1). Gọi D(a;b), khi đó ABCD là hình bình hành
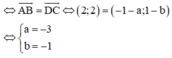
Suy ra số phức z biểu diễn D là z = -3 - i
Đáp án A

Ta có điểm A(0;-1), B(2;1), C(-1;1). Gọi D(a;b), khi đó ABCD là hình bình hành
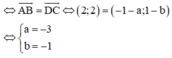
Suy ra số phức z biểu diễn D là z = -3 - i
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = − i ; z 2 = 2 + i ; z 3 = − 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành.
A. z = − 3 − i
B. z = − 2 − i
C. z = − 3
D. z = - 1 − 3 i
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB
![]()
![]()
![]()
![]()
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn z + 2 i - 1 = z + i Mô dul của số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A (1;3) là
A. 10
B. 7
C. 2 3
D. 2 5
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn z + 2 i − 1 = z + i . Mô dun của số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3) là
A. 10
B. 7
C. 2 3
D. 2 5
Cho số phức z thỏa mãn: z − 1 + i = 2 . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z là:
A. Một đường thẳng
B. Một đường Parabol
C. Một đường tròn có bán kính bằng 2
D. Một đường tròn có bán kính bằng 4
Trong mặt phẳng tọa độ Oxy, cho số phức z thỏa mãn z - 1 + 2 i = 3 . Tập hợp các điểm biểu diễn cho số phức w=z(1+i) là đường tròn
A. Tâm I(3;-1); R = 3 2
B. Tâm I(3;-1);R=3
C. Tâm I(-3;1); R = 3 2
D. Tâm I(3;-1);R=3
Xét các số phức z thỏa mãn điều kiện z - 1 + i = 2 Trong mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức w = z + 2 -i là
A. đường tròn tâm I(-3;2), bán kính R = 2.
B. đường tròn tâm I(3;-2), bán kính R = 2.
C. đường tròn tâm I(1;0), bán kính R =2.
D. đường tròn tâm I(1;-1), bán kính R = 2.
Gọi A,B,C là điểm biểu diễn các số phức z = 2 i ; z = 2 + i ; z = − 3 i . Khi đó diện tích tam giác ABC là
A. 7
B. 5
C. 6
D. 4
Tập hợp những điểm M trên mặt phẳng phức biểu diễn số phức z thỏa mãn z + 1 - i + z - 2 + 3 i = 10 có phương trình là
A. x = 2
B. x 2 25 + 4 y 2 75 = 1
C. x 2 25 + 2 y 2 33 = 1
D. Đ á p á n k h á c