x + m + 1 y = 1 4 x − y = − 2 ⇔ y = 4 x + 2 x + m + 1 4 x + 2 = 1 ⇔ y = 4 x + 2 x + 4 x m + 1 + 2 m + 1 = 1 ⇔ y = 4 x + 2 x 4 m + 5 = − 2 m + 1

Nếu m = − 5 4 ⇒ 0 x = 3 2 (vô lý)

Nếu m ≠ − 5 4 ⇒ x = − 2 m − 2 4 m + 5 ⇒ y = 4 x + 2 = 6 4 m + 5

Theo bài ra:  x 2 + y 2 = 1 4 ⇒ − 2 m − 1 4 m + 5 2 + 6 4 m + 5 2 = 1 4

⇔ 4 ( 4 m 2 + 4 m + 1 + 36 ) = 16 m 2 + 40 m + 25   ⇔ 24 m = 124 ⇔ m = 41 8

Đáp án:A

a) Thay \(m=7\) vào phương trình, ta được:

\(x^2-2x+7=0\)

Xét \(\Delta=\left(-2\right)^2-4.1.7=4-28=-24\)

=> Phương trình vô nghiệm \(\left(\Delta< 0\right)\)

b) Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2\right)}{1}=2\\x_1.x_2=\dfrac{m}{1}\end{matrix}\right.\)

Xét \(\Delta=\left(-2\right)^2-4.1.m=4-4m\)

Để phương trình có nghiệm thì \(\Delta\ge0\)

\(\Leftrightarrow4-4m\ge0\\ \Leftrightarrow-4m\ge-4\\ \Leftrightarrow m\le1\)

Theo đề bài, ta có: 

\(x^2+y^2=5\\ \Leftrightarrow x^2+y^2+2xy-2xy=5\\ \Leftrightarrow\left(x+y\right)^2-2xy=5\\ \Leftrightarrow2^2-2m=5\\ \Leftrightarrow4-2m=5\\ \Leftrightarrow2m=-1\\ \Leftrightarrow m=-\dfrac{1}{2}\)

\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)

\(\Rightarrow M\le9\)

\(M_{max}=9\) khi \(\left\{{}\begin{matrix}x+y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-\sqrt{3};\sqrt{3}\right);\left(\sqrt{3};-\sqrt{3}\right)\)

\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{\dfrac{1}{3}\left(x^2+y^2+xy\right)+\dfrac{2}{3}\left(x^2+y^2-2xy\right)}{x^2+y^2+xy}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\)

\(\Rightarrow M\ge1\)

\(M_{min}=1\) khi \(\left\{{}\begin{matrix}x-y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow x=y=\pm1\)

Đáp án A.

Điều kiện để phương trình đã cho là phương trình đường tròn là: 

m − 3 2 2 + ​   2 m + ​ 1 2 2 − ( 3 m + ​ 10 ) > 0 ⇔ m 2 − 6 m + ​ 9 4 + ​​​   4 m 2 + ​ 4 m + ​ 1 4 − 3 m − 10 > 0 ⇔ 5 m 2 − 2 m + ​ 10 4 ​​​  − 3 m − 10 > 0 ⇔ 5 m 2 − 2 m + 10 − 12 m − 40 > ​   0 ⇔ 5 m 2    − 14 m − 30 > ​ 0 ⇔ m < ​ 7 − 199 5 m > 7 + ​   199 5

Với điều  kiện trên phương trình đã cho là  phương trình đường tròn  có  tâm  I − m − 3 2 ;    − 2 m + 1 2

Do tâm I nằm trên đường thẳng ∆:   x + 2y + 5 = 0 nên ta có:

− m − 3 2 +   ​ 2.   − 2 m + 1 2 + ​   5 = 0 ⇔ − ( m − 3 ) + ​   2 ( ​ − 2 m − 1 ) + 2.5 = 0 ⇔ − m + ​ 3    − 4 m − 2 +   ​ 10 = 0    ⇔ − 5 m   ​ + ​ 11 = 0 ⇔ m   =    11 5

Kết hợp điều kiện, suy ra không có giá trị nào của m thỏa mãn,

Chú ý. Nhiều học sinh quên điều kiện để phương trình là phương trình của một đường tròn nên dẫn đến kết quả m = 11/5

ĐÁP ÁN D

Chọn đáp án D

Đáp án A

Phương pháp

Giả sử mặt phẳng (b) cắt mặt cầu (S ) theo đường tròn có bán kính r

Mặt cầu (S) có tâm I, bán kính R và d(I; β ) = R ta có   R 2 = r 2 + d 2

Cách giải

Mặt phẳng (b) cắt mặt cầu (S) theo đường tròn có bán kính  r = 8 π 2 π = 4

Mặt cầu (S) có tâm I(-1;2;3) bán kính  R = 17 - m

Ta có 

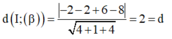
Áp dụng định lí Pytago ta có