Bài 7:

Ta có: \(AN=ND=\frac{AD}{2}\)

\(BC=\frac{AD}{2}\)

Do đó: AN=ND=BC

Xét tứ giác BNDC có

DN//BC

DN=BC

Do đó: BNDC là hình bình hành

=>BN//CD

mà CD⊂(SCD)

nên BN//(SCD)

Xét ΔSAD có

M,N lần lượt là trung điểm của AS,AD
=>MN là đường trung bình của ΔSAD

=>MN//SD

mà SD⊂(SCD)

nên MN//(SCD)

BN//(SCD)

MN//(SCD)

mà BN,MN cùng thuộc mp(BMN)

nên (BMN)//(SCD)

=>BM//(SCD)

Bài 6:

a: Xét ΔOAD và ΔOCB có

\(\hat{OAD}=\hat{OCB}\) (hai góc so le trong, AD//BC)

\(\hat{AOD}=\hat{COB}\) (hai góc đối đỉnh)

Do đó: ΔOAD~ΔOCB

=>\(\frac{OA}{OC}=\frac{OD}{OB}=\frac{AD}{BC}=2\)

=>\(BO=\frac12BD\) và OA=2OC

Xét ΔASC có \(\frac{AM}{MS}=\frac{AO}{OC}\left(=2\right)\)

nên MO//SC

=>MO//(SCD)

Xét ΔBSD có

\(\frac{BN}{NS}=\frac{BO}{OD}\left(=\frac12\right)\)

nên NO//SD

=>NO//(SCD)

mà MO//(SCD)

và NO,MO cùng thuộc mp(OMN)

nên (OMN)//(SCD)

4 x 3 = 12

4 X 3 =12

Các anh chj nhớ k e sẽ k lại

4 x 3 =12

MAGICPENCIL

HÃY LUÔN ;-)

Trả lời :

4x3=12

Đổi tk vx mk nha

Thiên_Hy

chời móa ơi vừa hc xong bài này lun

nhưng mừ

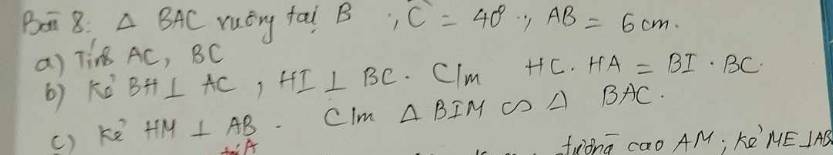
a: ΔABC vuông tại B

=>\(\widehat{A}+\widehat{C}=90^0\)

=>\(\widehat{A}=50^0\)

Xét ΔBAC vuông tại B có

\(sinC=\dfrac{AB}{AC}\)

=>\(AC=\dfrac{6}{sin40}\simeq9,33\left(cm\right)\)

ΔBAC vuông tại B

=>\(BA^2+BC^2=AC^2\)

=>\(BC=\sqrt{9.33^2-6^2}\simeq7,14\left(cm\right)\)

b: ΔBAC vuông tại B có BH là đường cao

nên \(HC\cdot HA=BH^2\left(1\right)\)

ΔBHC vuông tại H có HI là đường cao

nên \(BI\cdot BC=BH^2\left(2\right)\)

Từ (1),(2) suy ra \(HC\cdot HA=BI\cdot BC\)

c: ΔBHA vuông tại H có HM là đường cao

nên \(BM\cdot BA=BH^2\left(3\right)\)

Từ (2),(3) suy ra \(BI\cdot BC=BM\cdot BA\)

=>\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)

Xét ΔBIM vuông tại B và ΔBAC vuông tại B có

\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)

Do đó: ΔBIM đồng dạng với ΔBAC

\(\dfrac{20}{9}\)

= 20/9 bể

\(\dfrac{20}{9}\)bể

 y x 5 - 6 =1,9 x 3
y x 5 - 6 = 5,7
y x 5 = 5,7 + 6
y x 5 = 11,7
y = 11,7 : 5
y= 2,34

y x 5 - 6 = 5,7

y x 5 = 11,7

y = \(\dfrac{117}{50}\)

Câu 3:

a: Xét ΔSCD có

F là trung điểm của CD

J là trọng tâm

Do đó: \(\frac{SJ}{SF}=\frac23\)

=>Đúng

b: Xét ΔSAB có

SE là đường trung tuyến

I là trọng tâm

Do đó: S,I,E thẳng hàng

=>\(SI=\frac23SE\)

Xét ΔSFE có \(\frac{SI}{SE}=\frac{SJ}{SF}\left(=\frac23\right)\)

nên IJ//EF

mà EF⊂(ABCD)

nên JI//(ABCD)

=>Đúng

c: BC//AD

AD⊂(SAD)

BC không thuộc mp(SAD)

Do đó: BC//(SAD)

Ta có: \(AE=EB=\frac{AB}{2}\)

\(DF=FC=\frac{DC}{2}\)

mà AB=CD

nên AE=EB=DF=FC

Xét tứ giác BEFC có

BE//FC
BE=FC

Do đó: BEFC là hình bình hành

=>EF//BC

=>BC//(SEF)

=>Đúng

d: Sai

Câu 4:

a: Sửa đề: O là tâm của đáy ABCD

ABCD là hình chữ nhật

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét ΔDAB có

I,O lần lượt là trung điểm của DA,DB

=>IO là đường trung bình của ΔDAB

=>IO//AB

mà OI không thuộc mp(SAB) và AB⊂(SAB)

nên OI//(SAB)

=>Đúng

b: Vì OI//AB

mà AB//CD
nên OI//CD
mà OI không thuộc mp(SCD) và CD⊂(SCD)

nên OI//(SCD)

=>Đúng

c: Vì \(\frac{DI}{DA}<>\frac{DE}{DC}\)

nên IE không song song với AC

=>Sai

d: Gọi K là giao điểm của DG và SA

Xét ΔSAD có

G là trọng tâm

DG cắt SA tại K

Do đó: K là trung điểm của SA

Xét ΔSAD có

K là trung điểm của SA

G là trọng tâm

Do đó: \(DG=\frac23DK\)

Vì \(\frac{DG}{DK}<>\frac{DE}{DC}\left(\frac23<>\frac13\right)\)

nên GE không song song với KC

mà KC⊂(SBC)

nên GE không song với mp(SBC)

=>SAi

10+10=20

TL +20 nha

t đang cày sp nên xin tích

học tốt

thêm 1 dòng cho nó dài:)

10 + 10 = 20