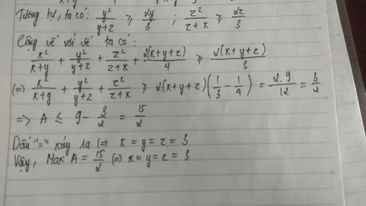nếu khó nhìn để mik đánh lại

Ta có:\(A=\dfrac{xy}{x+y}+\dfrac{yz}{y+z}+\dfrac{zx}{z+x}\)

             \(=\dfrac{x\left(x+y\right)-x^2}{x+y}+\dfrac{y\left(y+z\right)-y^2}{y+z}+\dfrac{z\left(z+x\right)-z^2}{z+x}\)

             \(=\left(x+y+z\right)-\left(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\right)\)

Ta có:\(\dfrac{x^2}{x+y}+\dfrac{x+y}{9}\ge2\sqrt{\dfrac{x^2}{x+y}.\dfrac{x+y}{9}}=\dfrac{2x}{3}\)

Tương tự,ta có:\(\dfrac{y^2}{y+z}+\dfrac{y+z}{9}\ge\dfrac{2y}{3};\dfrac{z^2}{z+x}+\dfrac{z+x}{9}\ge\dfrac{2z}{3}\)

Cộng vế với vế ta có:

\(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}+\dfrac{2\left(x+y+z\right)}{4}\ge\dfrac{2\left(x+y+z\right)}{3}\)

\(\Leftrightarrow\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\ge\dfrac{2\left(x+y+z\right)}{3}-\dfrac{2\left(x+y+z\right)}{4}=\dfrac{2.9}{3}-\dfrac{9}{2}=\dfrac{3}{2}\)

\(\Rightarrow A\le9-\dfrac{3}{2}=\dfrac{15}{2}\)

Dấu "=" xảy ra ⇔ x=y=z=3

Vậy,Max A=\(\dfrac{15}{2}\) ⇔ x=y=z=3

\(P=\Sigma\dfrac{x}{x+yz}=\Sigma\dfrac{x}{x(x+y+z)+yz}=\Sigma\dfrac{x}{x^2+xy+xz+yz} \\=\Sigma\dfrac{x}{(x+y)(x+z)}=\dfrac{2(xy+yz+zx)}{(x+y)(y+z)(z+x)}\)

Bất đẳng thức phụ: \(\Pi(x+y)\ge\dfrac{8}{9}(\Sigma x)(\Sigma xy)\)

\(\Leftrightarrow \Sigma(x^2y+x^2z-2xyz)\ge0\) ( đúng do AM-GM )

Dấu ''='' xảy ra khi và chỉ khi: \(x=y=z\)

Áp dụng vào bài toán chính: 

\(P\le\dfrac{2(xy+yz+zx)}{\dfrac{8}{9}(\Sigma x)(\Sigma xy)}=\dfrac{9}{4}\)

Dấu ''='' xảy ra khi và chỉ khi: \(x=y=z=\dfrac{1}{3}\)

Vậy \(\max P =\dfrac{9}{4} \) khi \(x=y=z=\dfrac{1}{3}\)

Không mất tính tổng quát, giả sử \(x=mid\left\{x;y;z\right\}\)

\(\Rightarrow\left(x-y\right)\left(x-z\right)\le0\)

\(\Rightarrow x^2+yz\le xy+xz\)

\(\Rightarrow zx^2+yz^2\le xyz+xz^2\)

\(\Rightarrow P\le x^3+y^3+z^3+8\left(xy^2+xz^2+xyz\right)\)

\(\Rightarrow P\le x^3+y^3+z^3+3yz\left(y+z\right)+8\left(xy^2+xz^2+2xyz\right)\)

\(\Rightarrow P\le x^3+\left(y+z\right)^3+8x\left(y+z\right)^2\)

\(\Rightarrow P\le x^3+\left(4-x\right)^3+8x\left(4-x\right)^2\)

\(\Rightarrow P\le8x^3-52x^2+80x+64\)

Tới đây, đơn giản nhất là khảo sát hàm \(f\left(x\right)=8x^3-52x^2+80x+64\) trên \(\left[0;4\right]\)

(Nếu ko khảo sát hàm, ta có thể tách như sau, tất nhiên là dựa trên điểm rơi có được từ việc khảo sát hàm):

\(\Rightarrow P\le\left(8x^3-52x^2+80x-36\right)+100\)

\(\Rightarrow P\le4\left(x-1\right)^2\left(2x-9\right)+100\)

Do \(0\le x\le4\Rightarrow2x-9< 0\Rightarrow P\le100\)

Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(1;3;0\right)\) và 1 vài bộ hoán vị của chúng

Bạn tham khảo:

Câu hỏi của Online Math - Toán lớp 8 | Học trực tuyến

bạn nào giúp mình tìm max thôi ^_^ còn min thì mình tìm được rồi 

tks ! 

nếu tìm được rồi thì giúp mình giải bài toán mới đăng đi

max =kxyz

min = xy

1 dung nha

sai đề

Theo nguyên lý Dirichlet, trong 3 số x;y;z luôn có 2 số cùng phía so với \(\dfrac{1}{2}\)

Không mất tính tổng quát, giả sử đó là y và z 

\(\Rightarrow\left(y-\dfrac{1}{2}\right)\left(z-\dfrac{1}{2}\right)\ge0\Leftrightarrow yz-\dfrac{1}{2}\left(y+z\right)+\dfrac{1}{4}\ge0\)

\(\Leftrightarrow y+z-yz\le\dfrac{1}{2}+yz\)

Mặt khác từ giả thiết:

\(1-x^2=y^2+z^2+2xyz\ge2yz+2xyz\)

\(\Leftrightarrow\left(1-x\right)\left(1+x\right)\ge2yz\left(1+x\right)\)

\(\Leftrightarrow1-x\ge2yz\)

\(\Rightarrow yz\le\dfrac{1-x}{2}\)

Do đó:

\(A=yz+x\left(y+z-yz\right)\le yz+x\left(\dfrac{1}{2}+yz\right)=\dfrac{1}{2}x+yz\left(x+1\right)\le\dfrac{1}{2}x+\left(\dfrac{1-x}{2}\right)\left(x+1\right)\)

\(\Rightarrow A\le-\dfrac{1}{2}x^2+\dfrac{1}{2}x+\dfrac{1}{2}=-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{8}\le\dfrac{5}{8}\)

\(A_{max}=\dfrac{5}{8}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{2};\dfrac{1}{2}\right)\)

\(\dfrac{xy^2}{y^2+2}=\dfrac{xy^2}{\dfrac{y^2}{2}+\dfrac{y^2}{2}+2}\le\dfrac{xy^2}{3\sqrt[3]{\dfrac{y^4}{2}}}=\dfrac{1}{3}x\sqrt[3]{2y^2}\le\dfrac{1}{9}x\left(2+y+y\right)=\dfrac{2}{9}\left(x+xy\right)\)

Tương tự: \(\dfrac{yz^2}{z^2+2}\le\dfrac{2}{9}\left(y+yz\right)\) ; \(\dfrac{zx^2}{x^2+2}\le\dfrac{2}{9}\left(z+zx\right)\)

Cộng vế:

\(P\le\dfrac{2}{9}\left(x+y+z+xy+yz+zx\right)\le\dfrac{2}{9}\left(x+y+z+\dfrac{1}{3}\left(x+y+z\right)^2\right)=4\)

Dấu "=" xảy ra khi \(x=y=z=2\)

\(xy+yz+zx=8xyz\Rightarrow\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=8\)

\(\Rightarrow\dfrac{8}{x}+\dfrac{8}{y}+\dfrac{8}{z}=64\)

Ta có: \(\dfrac{8}{x}+\dfrac{8}{y}+\dfrac{8}{z}\)

\(=\left(\dfrac{1}{x}+...+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)+\left(\dfrac{1}{y}+...+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{x}\right)+\left(\dfrac{1}{z}+...+\dfrac{1}{z}+\dfrac{1}{x}+\dfrac{1}{y}\right)\)

(sau dấu chấm là bốn số tương tự).

\(\ge^{Cauchy-Schwarz}\dfrac{8^2}{6x+y+z}+\dfrac{8^2}{6y+z+x}+\dfrac{8^2}{6z+x+y}\)

\(\Rightarrow64\ge\dfrac{8^2}{6x+y+z}+\dfrac{8^2}{6y+z+x}+\dfrac{8^2}{6z+x+y}\)

\(\Rightarrow\dfrac{1}{6x+y+z}+\dfrac{1}{6y+z+x}+\dfrac{1}{6z+x+y}\le1\)

Dấu "=" xảy ra khi \(x=y=z=\dfrac{3}{8}\)

Vậy \(Max\) của biểu thức đã cho là 1.