Tìm số nguyên x,y biết xy+x+y=27

Những câu hỏi liên quan
Tìm các cặp số nguyên x, y biết: x y = 2 7
Áp dụng Tính chất cơ bản của phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho:
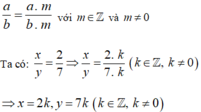
Đúng 0
Bình luận (0)
Tìm các số nguyên x , y biết 3x -2y = 27-xy
3x-2y=27-xy
3x-2y+xy=27
3x+xy-2y=27
x(3+y)-2y-6=27-6
x(3+y)-(2y+6)=21
x(3+y)-2(y+3)=21
(y+3)(x-2)=21
Ta có bảng giá trị:
| y+3 | 1 | 21 | 7 | 3 | -1 | -21 | -3 | -7 |
| y | -2 | 18 | 4 | 0 | -4 | -24 | -6 | -10 |
| x-2 | 21 | 1 | 3 | 7 | -21 | -1 | -7 | -5 |
| x | 23 | 3 | 5 | 9 | -19 | 1 | -5 | -3 |
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) tìm các số nguyên x y biết
(x-3)(xy-1)=7
b)tìm các số nguyên x y biết
y<0 và (x-3)×y=5
c)Tìm các Ư của A biết
A=1-4+5-8+9-12+...+27-30
d) tìm số nguyên x biết
(X-10)+(x-9)+(x-8)+...+(x-1)=-2015
Câu 6 Tìm số nguyên x, y biết : xy + 3x - y = 6
Câu 7 Tìm x, y, z biết : ![]() (x, y, z
(x, y, z ![]() )
)
\(xy+3x-y=6\\ \Rightarrow x\left(y+3\right)-y-3=3\\ \Rightarrow x\left(y+3\right)-\left(y+3\right)=3\\ \Rightarrow\left(x-1\right)\left(y+3\right)=3\)
Vì \(x,y\in Z\Rightarrow\left\{{}\begin{matrix}x-1,y+3\in Z\\x-1,y+3\inƯ\left(3\right)\end{matrix}\right.\)
Ta có bảng:
| x-1 | -1 | -3 | 1 | 3 |
| y+3 | -3 | -1 | 3 | 1 |
| x | 0 | -2 | 2 | 4 |
| y | -6 | -4 | 0 | -2 |
Vậy \(\left(x,y\right)\in\left\{\left(0;-6\right);\left(-2;-;\right);\left(2;0\right);\left(4;-2\right)\right\}\)
Đúng 5
Bình luận (0)
\(xy+3x-y=6\)
⇒ \(x\left(y+3\right)-\left(y+3\right)=3\)
⇒ \(\left(x-1\right)\left(y+3\right)=3\)
Đến đây em tự xét các trường hợp nha
Đúng 3
Bình luận (0)
Tìm số nguyên x, y sao cho 5x-2y+xy-27=0
Lời giải:
$5x-2y+xy-27=0$
$\Rightarrow (5x+xy)-2y-27=0$
$\Rightarrow x(y+5)-2(y+5)-17=0$
$\Rightarrow (x-2)(y+5)=17$
Do $x,y$ nguyên nên $x-2, y+5$ cũng là số nguyên. Mà tích của chúng bằng 17 nên xét các TH sau:
TH1: $x-2=1, y+5=17\Rightarrow x=3; y=12$
TH2: $x-2=-1, y+5=-17\Rightarrow x=1; y=-22$
TH3: $x-2=17, y+5=1\Rightarrow x=19; y=-4$
TH4: $x-2=-17, y+5=-1\Rightarrow x=-15; y=-6$
Đúng 0
Bình luận (0)
Tìm các số nguyên x,y biết
xy -y + y = 7
xy + x - y = 9
xy -x - y = 11
a) Tìm cặp số nguyên ( x,y) thỏa mãn x+y+xy=2
b) Tìm giá trị lơn nhất biểu thức \(Q=\frac{27-2x}{12-x}\)( với x nguyên )
a)x+y+xy=2
=> x+xy+y=2
=>x(y+1)+y=2
=>x(y+1)+y+1=3
=>x(y+1)+(y+1)=3
=>(y+1)(x+1)=3
Đến đây thì dễ rồi, bạn tự tìm nốt nha
b) \(\frac{27-2x}{12-x}=\frac{24-2x+3}{12-x}=\frac{2.\left(12-x\right)+3}{12-x}=2+\frac{3}{12-x}\)
Để Q lớn nhất thì \(\frac{3}{12-x}\) lớn nhất
Với x>12 thì \(\frac{3}{12-x}< 0\)
Với x<12 thì \(\frac{3}{12-x}.>0\)
Phân số \(\frac{3}{12-x}\) với x<12 có tử và mẫu đều dương, tử ko đổi nên mẫu phải nhỏ nhất
=>12-x=1
=>x=11
Đúng 0
Bình luận (0)
Tìm các cặp số (x;y) nguyên dương thỏa mãn xy+2x=27-3y
Bài này dễ mà!
Có: \(xy+2x=27-3y\)
\(x\left(y+2\right)=33-3\left(y+2\right)\)
\(x\left(y+2\right)+3\left(y+2\right)=33\)
\(\left(x+3\right)\left(y+2\right)=33\)
Đến phần này chắc bạn tự làm đc rồi nhỉ
Đúng 0
Bình luận (1)
Tìm tất cả các cặp số nguyên x,y sao cho : xy+7x-3y-27=0
Xem chi tiết
mình chỉ biết x=3,857142857
a, Tìm cặp số nguyên (x,y) thỏa mãn x + y + xy = 2
b, Tìm giá trị lớn nhất của biểu thức \(Q=\frac{27-2x}{12-x}\)
với x nguyên.
x + y + xy = 2
=> (x + xy) + (y + 1) = 3
=> (y + 1)(x + 1) = 3
=> [(x + 1),(y + 1)] = (1,3;3,1;-1,-3;-3,-1)
=> (x,y) = (0,2;0,2;-2,-4;-4,-2)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

























