Nếu abcd + bcda + cdab + dabc = 17776. Tính a + b + c + d

Những câu hỏi liên quan
Nếu \(ab\times5=cd\) và \(ac\times b=adc\) thì \(abcd+bcda+cdab+dabc=?\)
Bài 6: Cho DABC cân tại A có AB = 3cm, BC= 3√2cm, D là điểm đối xứng với A qua BC.
a)Chứng minh DABC vuông cân tại A.
b)Chứng minh tứ giác ABCD là hình bình hành.
c)Hình bình hành ABCD có hình vuông không ? Vì sao ?
Trong không gian cho hình chữ nhật ABCD có
A
B
a
,
A
C
a
5
. Tính diện tích xung quanh
S
x
q
của hình trụ khi quay đường gấp khúc BCDA quanh trục AB A.
S
x
q
2
π
a
2
.
B. ...
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có A B = a , A C = a 5 . Tính diện tích xung quanh S x q của hình trụ khi quay đường gấp khúc BCDA quanh trục AB
A. S x q = 2 π a 2 .
B. S x q = 4 π a 2 .
C. S x q = 2 a 2 .
D. S x q = 4 a 2 .
Trong không gian cho hình chữ nhật ABCD có
A
B
a
,
A
C
a
5
. Tính diện tích xung quanh
S
x
q
của hình trụ khi quay đường gấp khúc BCDA quanh trục AB. A.
S
x
q
2
π
a
2
.
B....
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có A B = a , A C = a 5 . Tính diện tích xung quanh S x q của hình trụ khi quay đường gấp khúc BCDA quanh trục AB.
A. S x q = 2 π a 2 .
B. S x q = 4 π a 2 .
C. S x q = 2 a 2 .
D. S x q = 4 a 2 .
Đáp án B
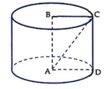
Khi quay đường gấp khúc BCDA quanh trục AB, ta được một hình trụ có bán kính đáy
R = B C = A C 2 − A B 2 = a 5 2 − a 2 = 2 a
chiều cao h = A B = a .
Diện tích xung quanh của hình trụ là: S x q = 2 π R h = 2 π .2 a . a = 4 π a 2
Đúng 0
Bình luận (0)
Trong không gian cho hình chữ nhật ABCD có
A
B
a
,
A
C
a
5
. Tính diện tích xung quanh
S
x
q
của hình trụ khi quay đường gấp khúc BCDA quanh trục AB A.
S
x
q
2
π
a
2
.
B.
S
x...
Đọc tiếp
Trong không gian cho hình chữ nhật ABCD có A B = a , A C = a 5 . Tính diện tích xung quanh S x q của hình trụ khi quay đường gấp khúc BCDA quanh trục AB
A. S x q = 2 π a 2 .
B. S x q = 4 π a 2 .
C. S x q = 2 a 2 .
D. S x q = 4 a 2 .
Tứ giác ABCD có góc A=B,BC=AC
a)CM: tam giácDAB=CBAtừ đó =)BD=AC
b)CM: góc ADC=BCD
c)AB\\CD
ABCD có góc A = góc B
=> ABCD là hình thang cân
=> AC = BD (2 dg chéo = nhau)
=> AD = BC (2 cạnh bên = nhau)
a/ Xét 2 tam giác: DAB và CBA có:
AB cạnh chung
AD = BC
AC = BD
=> tam giác DAB = tam giác CBA (c.c.c)
=> BD = AC (2 cạnh tương ứng = nhau) đpcm
b/
Xét 2 tam giác: ADC và BCD có:
CD cạnh chung
AD = BC
AC = BD
=> tam giác ADC = tam giác BCD (c.c.c)
=> Góc ADC = góc BCD (2 góc tương ứng = nhau)
c/ hình thang cân có 2 đáy // với nhau
=> AB // CD
Đúng 0
Bình luận (1)
Câu 6. Cho DABC DDEF . Chọn câu sai ? A. AB DE . B. A D C. BC DF D. BC EF . Câu 7. Cho DABC vuông tại A, AH ^ BC ( H Î BC ); AB 9 cm, AH 7, 2 cm, HC 9, 6 cm. Tính cạnh AC; BC . A. AC 15 cm; BC 12 cm . B. AC 12 cm; BC 14, 5 cm C. AC 12 cm; BC 15 cm D. AC 10 cm; BC 15 cm . Câu 8. Cho DDEF DMNP . Biết rằng độ dài cạnh FD : EF + FD 10 cm, NP - MP 2 cm và DE 3 cm. Tính A. 4 cm B. 6 cm C. 8 cm ...
Đọc tiếp
Câu 6. Cho DABC = DDEF . Chọn câu sai ?
A. AB = DE . B. A = D
C. BC = DF
D. BC = EF .
Câu 7. Cho
DABC
vuông tại A,
AH ^ BC
( H Î BC );
AB = 9 cm,
AH = 7, 2 cm,
HC = 9, 6 cm.
Tính cạnh
AC;
BC .
A. AC = 15 cm;
BC = 12 cm . B. AC = 12 cm;
BC = 14, 5 cm
C. AC = 12 cm; BC = 15 cm
D. AC = 10 cm;
BC = 15 cm .
Câu 8. Cho DDEF = DMNP . Biết rằng độ dài cạnh FD :
EF + FD = 10 cm,
NP - MP = 2 cm và
DE = 3 cm. Tính
A. 4 cm B. 6 cm C. 8 cm D. 10 cm.
Câu 9. Cho tam giác ABC có M là trung điểm của BC và
AM = BC/2 , số đo góc BAC là:
A. 45° . B. 30° . C. 90° . D. 60° .
Xem thêm câu trả lời
abcd + 4707 = bcda
ai nhanh mik tick đúng cho
\(\overline{abcd}+4707=\overline{bcda}\)
\(\Rightarrow1000xa+\overline{bcd}+4707=10x\overline{bcd}+a\)
\(\Rightarrow999xa+4707=9x\overline{bcd}\)
\(\Rightarrow111xa+523=\overline{bcd}\)
Ta có \(\overline{bcd}\le999\Rightarrow111xa+523\le999\Rightarrow111xa\le999-523=476\)
\(\Rightarrow a\le4\)
+ Với \(a=0\Rightarrow\overline{bcd}=523\)
+ Với \(a=1\Rightarrow\overline{bcd}=111+523=634\)
+ Với \(a=2\Rightarrow\overline{bcd}=222+523=745\)
+ Với \(a=3\Rightarrow\overline{bcd}=333+523=856\)
+ Với \(a=4\Rightarrow\overline{bcd}=444+523=967\)
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD có AB 6cm, BC 8cm. Vẽ BH vuông góc với AC (H in AC )a) C/m: DeltaBHC sim DeltaCDAb) Tính diện tích DeltaBHCc) Gọi M, B lần lượt là trung điểm của AH và BH, tia MN cắt BC tại E. Chứng minh DeltaCEH sim DeltaCMB
Đọc tiếp
Cho hình chữ nhật ABCD có AB = 6cm, BC = 8cm. Vẽ BH vuông góc với AC (H \(\in\) AC )
a) C/m: \(\Delta\)BHC \(\sim\) \(\Delta\)CDA
b) Tính diện tích \(\Delta\)BHC
c) Gọi M, B lần lượt là trung điểm của AH và BH, tia MN cắt BC tại E. Chứng minh \(\Delta\)CEH \(\sim\) \(\Delta\)CMB
Cho dãy tỉ số bằng nhau :
\(\dfrac{a+bcd}{abcd}=\dfrac{b+cad}{bcad}=\dfrac{c+abd}{cabd}=\dfrac{d+abc}{dabc}\)
Chứng minh : \(\dfrac{bcd}{a}=\dfrac{cad}{b}=\dfrac{abd}{c}=\dfrac{abc}{d}\)