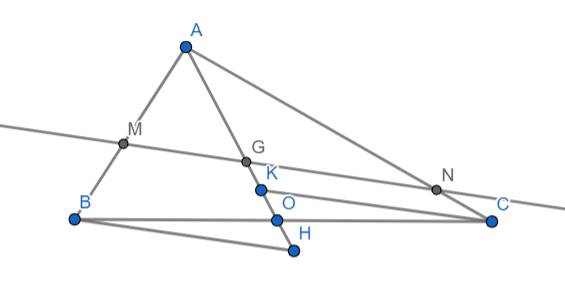
Xét 2 tam giác AMG và ABH ta có:

\(\widehat{BAH}\) chung 

\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG) 

\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\) 

\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1) 

Xét 2 tam giác ANG và ACK có:

\(\widehat{CAK}\) chung 

\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN) 

\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)

\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2) 

Xét hai tam giác BOH và COK ta có: 

\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh) 

\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC) 

\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK) 

\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\) 

\(\Rightarrow HO=OK\) (hai cạnh t.ứng) 

\(\Rightarrow HK=2HO\)

Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\) 

\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\) 

Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\) 

\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)  

Gọi J là trung điểm BC. Khi đó AJ là trung tuyến. Vậy thì AG = 2GJ.     (1)

Xét tứ giác BIKC có BI cùng CK cùng song song với AG nên BI // CK hay BIKC là hình thang.

Xét hình thang BIKC có :

J là trung điểm BC

GJ // BI // KC 

Suy ra GJ là đường trung bình hình thang BIKC.

Từ đó ta có: \(BI+CK=2GJ\)                    (2)

Từ (1) và (2) suy ra \(BI+KC=AG\)

hình tự vẽ nha bn! gọi K,I,P lần lượt là tđ của AB,AC,BC

ta có AG/AP=2/3=> S AMG/ABP=2/3=> AM/AB=2/3

ta có AM/AB=2/3,AG/AP=2/3=> MG//BP (định lý talet đảo)

khi MG//BP=> AB/AM=AP/AG (1)

khi GN//PC (MG//BP) => AP/AG=AC/AN (2)

từ (1),(2)=> AB/AM+AC/AN=2AP/AG=2.3/2=3

.

@ 肖战Daytoy_1005 giúp với

Gọi E là trung điểm KL; I là trung điểm AG

\(\left\{{}\begin{matrix}KE=EL\\BD=DC\end{matrix}\right.\Rightarrow ED\) là đtb hthang \(BCLK\left(BK//LC.do.cùng.\perp KL\right)\)

\(\Rightarrow ED=\dfrac{BK+CL}{2}\Rightarrow2ED=BK+CL\left(1\right)\)

Vì G là trọng tâm tam giác ABC nên \(GD=\dfrac{1}{2}AG\)

Mà \(AI=IG=\dfrac{1}{2}AG\) nên \(GD=AI=IG\)

Ta có \(ED//BK//LC\left(t/c.đtb\right)\Rightarrow ED\perp KL\left(BK\perp KL\right)\)

Áp dụng định lí Ta-lét cho \(AH//ED\left(\perp KL\right)\) ta có

\(\dfrac{AH}{ED}=\dfrac{AG}{GD}=2\Rightarrow AH=2ED\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AH=BK+CL\)