Giải chi tiết cho em ạ

Giải giúp mình với lời giải chi tiết ạ^^
Giải nhanh nhanh em tick cho ạ 
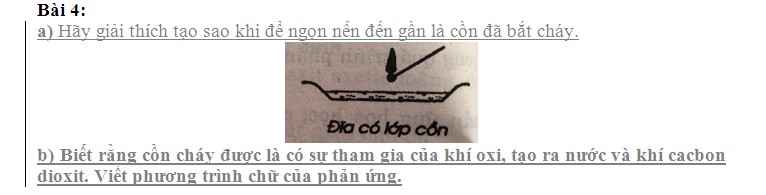 mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
mấy anh chị giải chi tiết giùm em,em cần lời giải chi tiết ạ em xin cảm ơn
Cho em lời giải chi tiết ạ
em cảm ơn mn 

Cho em lời giải chi tiết với ạ
Em cảm ơn 
\(n_{Fe}=\dfrac{11,2}{56}=0,2\left(mol\right)\\ n_S=\dfrac{3,2}{32}=0,1\left(mol\right)\\ PTHH:Fe+S\underrightarrow{t^o}FeS\left(1\right)\\ LTL:0,2>0,1\Leftrightarrow Fe.dư\)
\(Theo.pt\left(1\right):n_{Fe\left(pư\right)}=n_{FeS}=0,1\left(mol\right)\\ n_{FeS\left(dư\right)}=0,2-0,1=0,1\left(mol\right)\)
\(PTHH:FeS+H_2SO_4\rightarrow FeSO_4+H_2S\uparrow\left(2\right)\\ Fe+2H_2SO_4\rightarrow FeSO_4+SO_2\uparrow+2H_2O\left(3\right)\)
\(Theo.pt\left(2\right):n_{H_2S}=n_{FeS}=0,1\left(mol\right)\\ Theo.pt\left(3\right):n_{SO_2}=n_{Fe}=0,1\left(mol\right)\\ \%V_{H_2S}=\dfrac{0,1}{0,1+0,1}=50\%\\ \%V_{SO_2}=100\%-50\%=50\%\)
\(Theo.pt\left(2\right):n_{H_2SO_4\left(2\right)}=n_{FeS}=0,1\left(mol\right)\\ Theo.pt\left(3\right):n_{H_2SO_4\left(3\right)}=2n_{Fe}=2.0,1=0,3\left(mol\right)\\ C_{MddH_2SO_4}=\dfrac{0,3}{0,2}=1,5M\)
cho em xin bài giải chi tiết ạ
a: Xét tứ giác ABEC có
D là trung điểm của AE
D là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra:AB//CE
Cho em xin lời giải chi tiết ạ

cho em lời giải chi tiết với ạ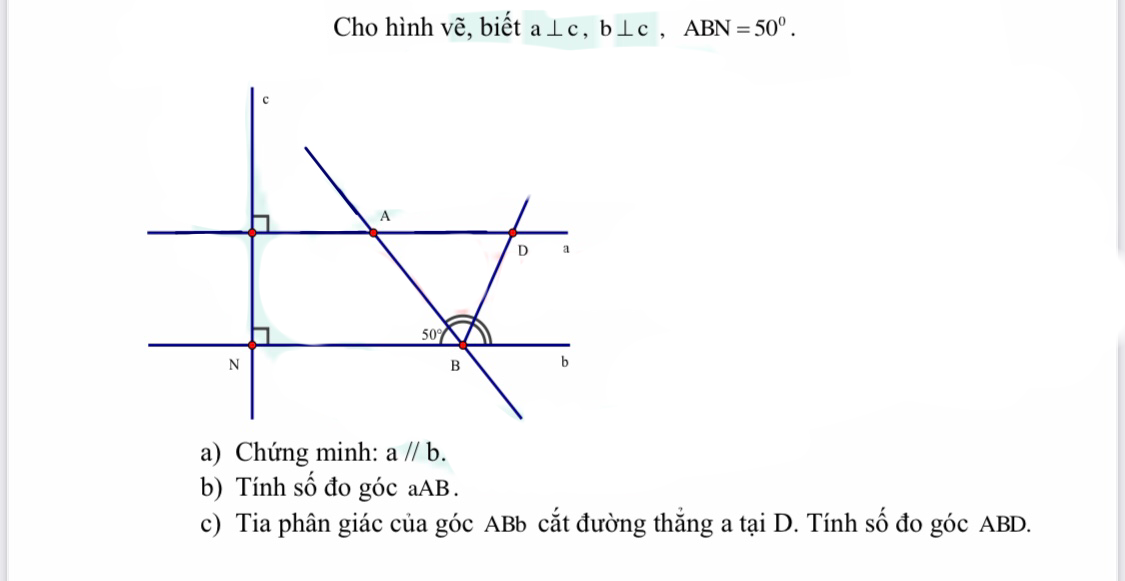
Giải hộ em ạ giải chi tiết ạ em cần gấp ạ 
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
b: ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
c: Ta có: \(\widehat{ADB}=90^0\)
=>AD\(\perp\)BC tại D
D là trung điểm của BC
=>\(DB=DC=\dfrac{BC}{2}=\dfrac{24}{2}=12\left(cm\right)\)
ΔADB vuông tại D
=>\(AD^2+DB^2=AB^2\)
=>\(AD^2=20^2-12^2=256\)
=>\(AD=\sqrt{256}=16\left(cm\right)\)
Xét ΔABC có
AD là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot16=\dfrac{32}{3}\left(cm\right)\)
 ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
ai giải giùm em câu 6 vs ạ cho em lời giải chi tiết và vẽ hình giúp em vs ạ cảm ơn mn
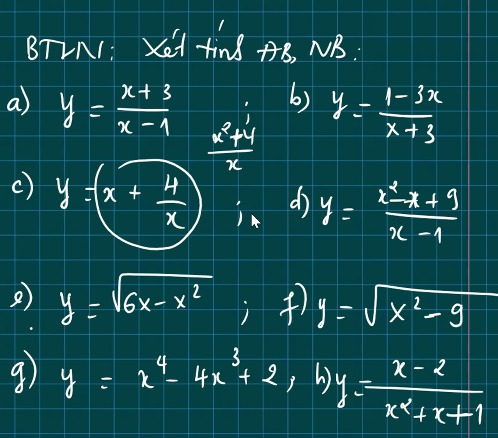 Cho em xin lời giải chi tiết với ạ
Cho em xin lời giải chi tiết với ạ
f.
TXĐ: \(x\in(-\infty;-3]\cup[3;+\infty)\)
\(y'=\dfrac{2x}{2\sqrt{x^2-9}}=\dfrac{x}{\sqrt{x^2-9}}\)
Dấu của y':

Hàm đồng biến trên \([3;+\infty)\) và nghịch biến trên \((-\infty;-3]\)
g.
\(y'=4x^3-12x^2=4x^2\left(x-3\right)=0\Rightarrow x=3\) (khi tìm khoảng đơn điệu hay cực trị của hàm số thì chỉ cần quan tâm nghiệm bội lẻ, không cần quan tâm nghiệm bội chẵn)
Dấu của y':
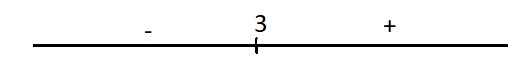
Hàm đồng biến trên \(\left(3;+\infty\right)\) và nghịch biến trên \(\left(-\infty;3\right)\)
h.
\(y'=\dfrac{x^2+x+1-\left(x-2\right)\left(2x+1\right)}{\left(x^2+x+1\right)^2}=\dfrac{-x^2+4x+3}{\left(x^2+x+1\right)^2}\)
\(y'=0\Leftrightarrow-x^2+4x+3=0\Rightarrow\left[{}\begin{matrix}x=2-\sqrt{7}\\x=2+\sqrt{7}\end{matrix}\right.\)
Dấu của y':
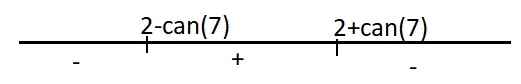
Hàm đồng biến trên \(\left(2-\sqrt{7};2+\sqrt{7}\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2-\sqrt{7}\right)\) và \(\left(2+\sqrt{7};+\infty\right)\)