 làm hộ mình
làm hộ mình

Những câu hỏi liên quan
làm hộ mình câu 5 hoặc câu 6 cũng được chứ câu 4 ko cần làm đâu nhé !
 Làm hộ mình câu 5 thôi nhé !
Làm hộ mình câu 5 thôi nhé !
làm hộ mình phép tính bằng cách tính nhanh nhé
6,7*9,55+9,45*16,7+16,7
làm hẳn ra hộ mình nhé
Làm hộ mình phép tính được không mình làm hết lời giải rồi mà mình không biết làm phép tính 
làm hộ mình câu này với(mình cần gấp),ai làm nhanh nhất mình tim cho .
Mấy bạn kiểm tra hộ mình trang đầu và làm hộ mình trang 2 với ạ , cho mình cảm ơn .Giúp mình nhanh với :(

exs1
1 don't have to
3 mustn't
7 don't have to
exs2
3 might
4 can't
7 might be
còn nữa ...
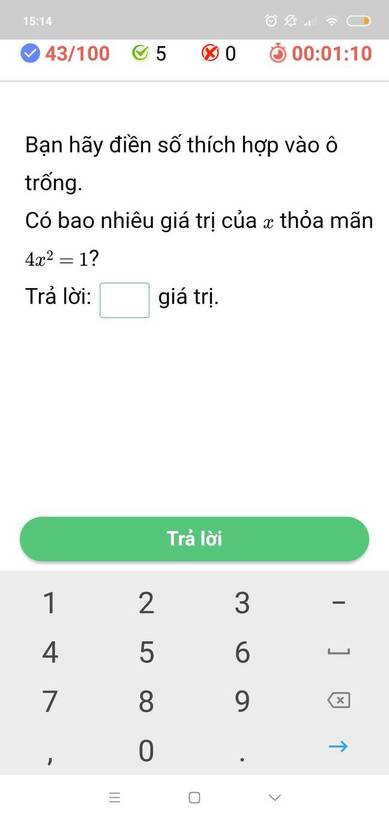 làm hộ mình nha làm luô
làm hộ mình nha làm luô
xin lỗi mk ko biết
chúc pro ngủ ngon
k đê
hok tốt
@@@@@@@@@@@@
có 2 giá trị là 1/2 cà -1/2
Xem thêm câu trả lời
Giúp mình làm chi tiết và đúng vs nhé làm hết hộ mình
Em chia nhỏ bài ra mỗi bài đăng 1 lượt hỏi nha!
Đúng 1
Bình luận (3)
Bài 6:
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
=>AM⊥DE
Đúng 0
Bình luận (1)
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp, làm nhanh hộ mình với ạ <3

ext-9bosssssssssssssssss
 Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều
Mọi người làm hộ mình bài 4,5,6 hộ mk cái nha...Mình cảm ơn các bạn rất nhiều![]()
Bài 4:
a) Vì $ABC$ cân tại $A$ nên $AB=AC$ và $\widehat{ABC}=\widehat{ACB}$
$\Rightarrow 180^0-\widehat{ABC}=180^0-\widehat{ACB}$
hay $\widehat{ABQ}=\widehat{ACR}$
Xét tam giác $ABQ$ và $ACR$ có:
$AB=AC$ (cmt)
$\widehat{ABQ}=\widehat{ACR}$ (cmt)
$BQ=CR$ (gt)
$\Rightarrow \triangle ABQ=\triangle ACR$ (c.g.c)
$\Rightarrow AQ=AR$
b)
$H$ là trung điểm của $BC$ nên $HB=HC$
Mà $QB=CR nên $HB+QB=HC+CR$ hay $QH=HR$
Xét tam giác $AQH$ và $ARH$ có:
$AQ=AR$ (cmt)
$QH=RH$ (cmt)
$AH$ chung
$\Rightarrow \triangle AQH=\triangle ARH$ (c.c.c)
$\Rightarrow \widehat{QAH}=\widehat{RAH}$
Đúng 1
Bình luận (0)
Bài 5:a)
Xét tam giác vuông $AHB$ và $AHC$ có:
$AB=AC$ (do $ABC$ là tam giác cân ở A)
$\widehat{ABH}=\widehat{ACH}$ (do tam giác $ABC$ cân ở A)
$\Rightarrow \triangle AHB=\triangle AHC$ (cạnh huyền- góc nhọn)
$\Rightarrow HB=HC$ và $\widehat{BAH}=\widehat{CAH}$ (đpcm)
b)
$HB=HC$ nên $H$ là trung điểm $BC$. Do đó $HB=BC:2=4$ (cm)
Áp dụng định lý Pitago:
$AH=\sqrt{AB^2-AH^2}=\sqrt{5^2-4^2}=3$ (cm)
c)
Xét tam giác vuông $ADH$ và $AEH$ có:
$AH$ chung
$\widehat{DAH}=\widehat{EAH}$ (do $\widehat{BAH}=\widehat{CAH}$)
$\Rightarrow \triangle ADH=\triangle AEH$ (cạnh huyền- góc nhọn)
$\Rightarrow DH=EH$ nên tam giác $HDE$ cân tại $H$.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
làm hộ mình , mình cần gấp
























