Cho biết các đỉnh của tam giác ABC (Hình 2) có thuộc đường tròn (O) hay không.
Cho tam giác ABC(AB<AC) nội tiếp trong đường tròn (O). Vẽ đường kính \(MN\perp BC\)( điểm M thuộc cung BC không chứa A).Chứng minh giằng các tia AM,AN lần lượt là tia phân giác trong và ngoài tại đỉnh A của tam giác ABC.
Vẽ hình hộ mình nhá
Chứng minh được B M ⏜ = M C ⏜ => AM là phân giác trong
Mặt khác: M A N ^ = 90 0
=> AN là phân giác ngoài
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O). Vẽ đường kính MN ^ BC (điểm M thuộc cung BC không chứa A). Chứng minh các tia AM, AN lần lượt là các tia phân giác các góc trong và các góc ngoài tại đỉnh A của tam giác ABC
Chứng minh được B M ⏜ = M C ⏜ => AM là phân giác trong
Mặt khác: M A N ^ = 90 0
=> AN là phân giác ngoài
Gọi O là giao điểm của ba đường trung trực của tam giác ABC (Hình 4). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không.
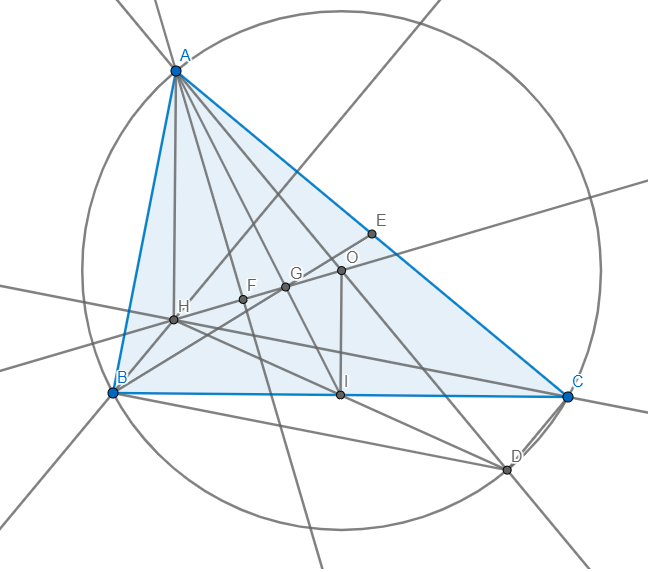
Cho tam giác ABC nhọn có ba đỉnh thuộc đường tròn (O). Gọi H là trực tâm của tam giác
ABC. Vẽ đường kính AD.
a) Tứ giác BHCK là hình gì?
b) Gọi I là trung điểm của BC. Chứng minh AH=2.OI
c) Gọi G là trọng tâm của tam giác ABC. Chứng minh 3 điểm H, G, O thẳng hàng và GH=2.GO
d) So sánh diện tích hai tam giác AHG và tam giác AOG.
a) chắc đề hỏi là tứ giác BHCD là hình gì chứ ko có điểm K
Vì AD là đường kính \(\Rightarrow\left\{{}\begin{matrix}\angle ACD=90\\\angle ABD=90\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}CD\bot AC\\BD\bot AB\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}BH\bot AC\\CH\bot AB\end{matrix}\right.\Rightarrow\) \(CD\parallel BH,BD\parallel CH\) \(\Rightarrow BHCD\) là hình bình hành
b) Vì BHCD là hình bình hành có I là trung điểm BC
\(\Rightarrow H,I,D\) thẳng hàng và I cũng là trung điểm HD
Xét \(\Delta AHD\) có O là trung điểm AD,I là trung điểm HD
\(\Rightarrow OI\) là đường trung bình \(\Rightarrow OI=\dfrac{1}{2}AH\Rightarrow AH=2OI\)
c) AI cắt HO tại G'.
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{AH}{OI}=\dfrac{AG'}{G'I}\Rightarrow\dfrac{AG'}{G'I}=2\Rightarrow\dfrac{AG'}{AI}=\dfrac{2}{3}\)
\(\Rightarrow G'\) là trọng tâm tam giác ABC \(\Rightarrow G\equiv G'\Rightarrow\) đpcm
Vì \(OI\parallel AH\) \(\Rightarrow\dfrac{GH}{GO}=\dfrac{AH}{OI}=2\Rightarrow GH=2GO\)
d) Kẻ \(AF\bot HO\) \(\Rightarrow\left\{{}\begin{matrix}S_{AOG}=\dfrac{1}{2}.AF.OG\\S_{AHG}=\dfrac{1}{2}.AF.HG\end{matrix}\right.\)
mà \(GH=2GO\Rightarrow S_{AHG}=2S_{AOG}\)
Cho tam giác ABC nội tiếp đường tròn (O) và M thuộc (O), không trùng
các đỉnh A, B, C. Gọi P, Q, R lần lượt là hình chiếu vuông góc của M xuống BC, CA,
AB. Biết góc MCP=74 độ , thế thì góc AQR = .?
Nối A → M; ta có góc ARM = góc AQM = 90° => tứ giác ARMQ nội tiếp
=> góc RAQ + góc RMQ = 180°
Lại có cung BAM = 74° => cung BCM = 360° - 74° = 286° => góc BAM = 1/2.cung BCM = 143°
Góc BAM bù với góc RAM => góc RAM = 180° - 143° = 33°
Góc RAM và góc RQM cùng chắn cung RM của đường tròn ngoại tiếp tứ giác AMRQ
=> góc RAM = góc RQM = 33°
Mà góc AQR phụ với góc RQM => góc AQR = 90° - 33° = 57°
Ta có: tứ giác AMBC nội tiếp đường tròn nên góc MCB= MAB=74 độ
Mặt khác, tứ giác QARM nội tiếp nên MAB =MQR=74 độ
Ta lại có: MQR+AQR =90 độ nên tính được AQR
trong hệ trục tọa độ oxy, cho đường tròn tâm O. Gọi H(-1;0) và K(1;1) lần lượt là chân các đường vuông góc kẻ từ B và C của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC, biết A thuộc d:3x-y-1=0
Tam giác ABC có góc A là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau ở O. Các điểm B và C có thuộc đường tròn tâm O bán kính OA hay không? Vì sao?
Từ giả thiết suy ra OA = OB = OC.
Vậy các điểm B và C có thuộc đường tròn tâm O bán kính OA.
cho tam giác ABC nội tiếp đường tròn tâm I, có đỉnh A thuộc đường thẳng d:x+y-2=0, điểm D(-2;1) là chân đường cao của tam giác ABC hạ từ A. Gọi E(3;1) là chân đường vuông góc hạ từ B xuống AI, điểm P(2;1) thuộc cạnh AC. Tìm tọa độ các đỉnh của tam giác ABC
Ta dễ có tứ giác ABDE nội tiếp đường tròn đường kính AB => ^CDE = ^BAE
Lại có ^BAE = ^CAD (= 900 - ^ACB), suy ra ^CDE = ^CAD = 900 - ^ACD => DE vuông góc AC
Thấy D,E,P cùng có tung độ bằng 1 => D,E,P thẳng hàng, vì P thuộc AC nên DE vuông góc với AC tại P
Đường thẳng AC: đi qua P(2;1), VTPT \(\overrightarrow{DE}=\left(5;0\right)\) \(\Rightarrow AC:x-2=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\x+y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\Rightarrow A\left(2;0\right)\)
Đường thẳng BC: đi qua \(D\left(-2;1\right)\),VTPT \(\overrightarrow{DA}=\left(4;-1\right)\Rightarrow BC:4x-y+9=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\4x-y+9=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=17\end{cases}\Rightarrow C\left(2;17\right)}\)
Đường thẳng BE: đi qua \(E\left(3;1\right)\), VTPT \(\overrightarrow{AE}=\left(1;1\right)\Rightarrow BE:x+y-4=0\)
Xét hệ: \(\hept{\begin{cases}4x-y+9=0\\x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\Rightarrow B\left(-1;5\right)\)
Vậy \(A\left(2;0\right),B\left(-1;5\right),C\left(2;17\right)\).
trong hệ trục tọa độ oxy, cho đường tròn tâm O. Gọi H(-1;0) và K(1;1) lần lượt là chân các đường vuông góc kẻ từ B và C của tam giác ABC. Tìm tọa độ các đỉnh của tam giác ABC, biết A thuộc d:3x-y-1=0
Cho tam giác ABC có cạnh AB là đường kính cố định của (O;R), đỉnh C di chuyển trên đường tròn đó. AM, BN là các đường trung tuyến. a) Chứng minh: AM^2+BN^2 không đổi
b) Tìm tập hợp trọng tâm G của tam giác ABC