Ai giúp em giải câu c,f,g với ạ

Giải giúp em câu bcdef với ạ riêng b,e,f giải đưa về cos giúp em
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
d.
\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sinx-\dfrac{\sqrt{2}}{2}cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
giúp em câu f,g với ạ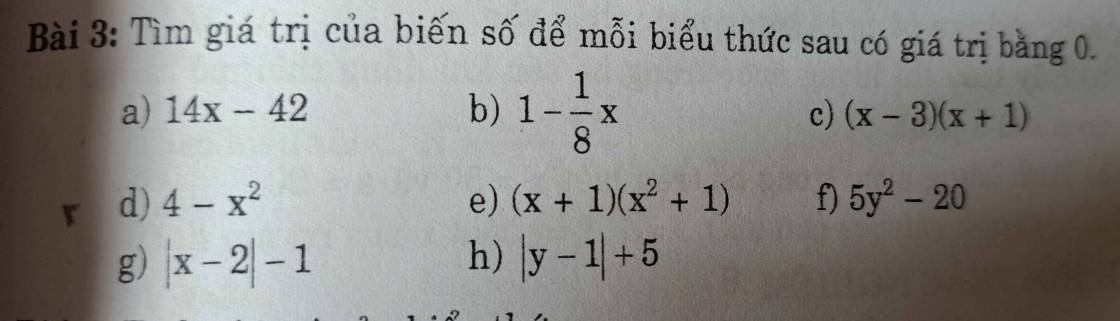
f: 5y^2-20=0
=>y^2-4=0
=>(y-2)(y+2)=0
=>y=2 hoặc y=-2
g: |x-2|-1=0
=>|x-2|=1
=>x-2=1 hoặc x-2=-1
=>x=3 hoặc x=1
Ai giúp em giải câu b, c, d với ạ
Có bài mẫu là câu a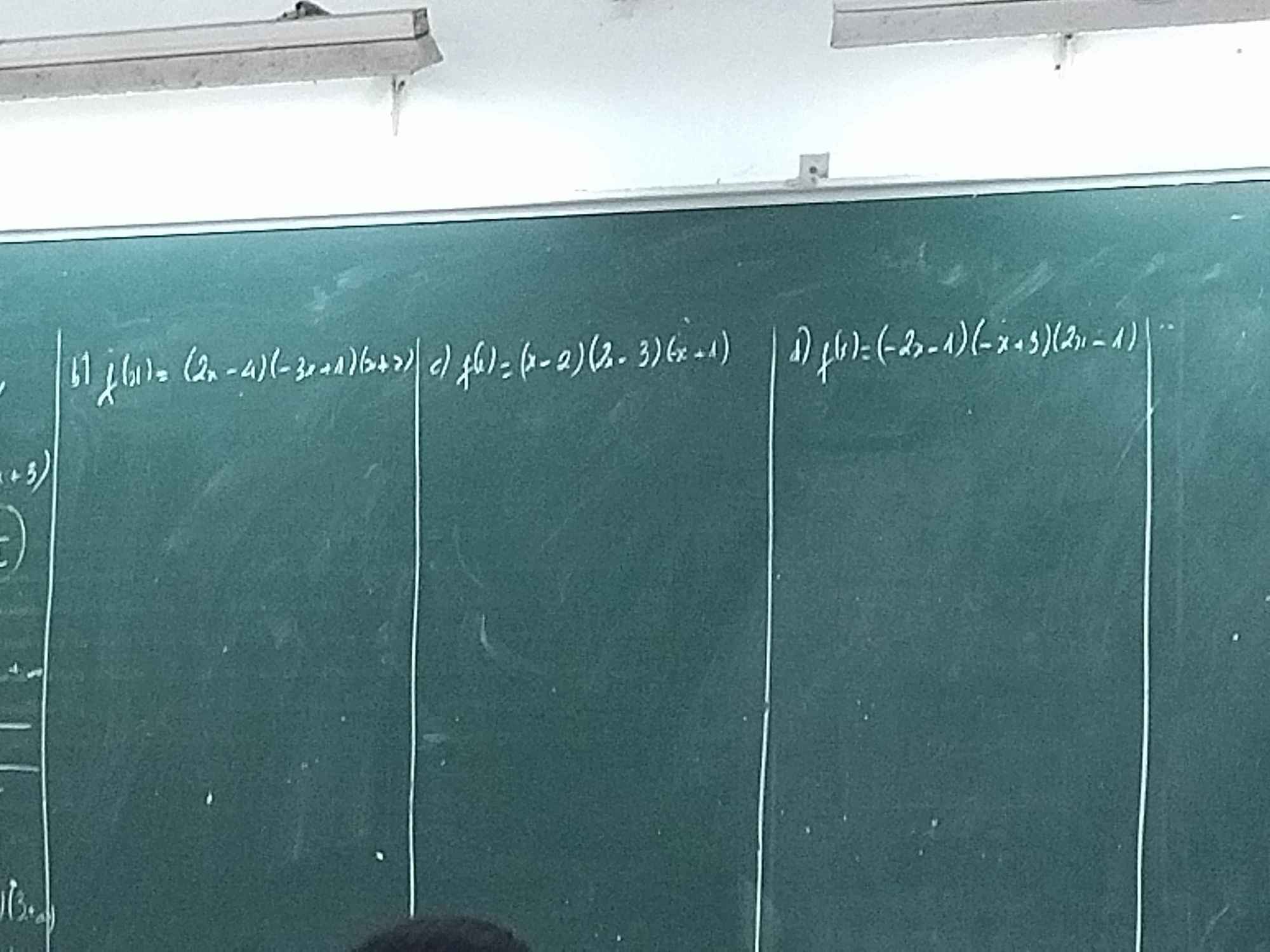
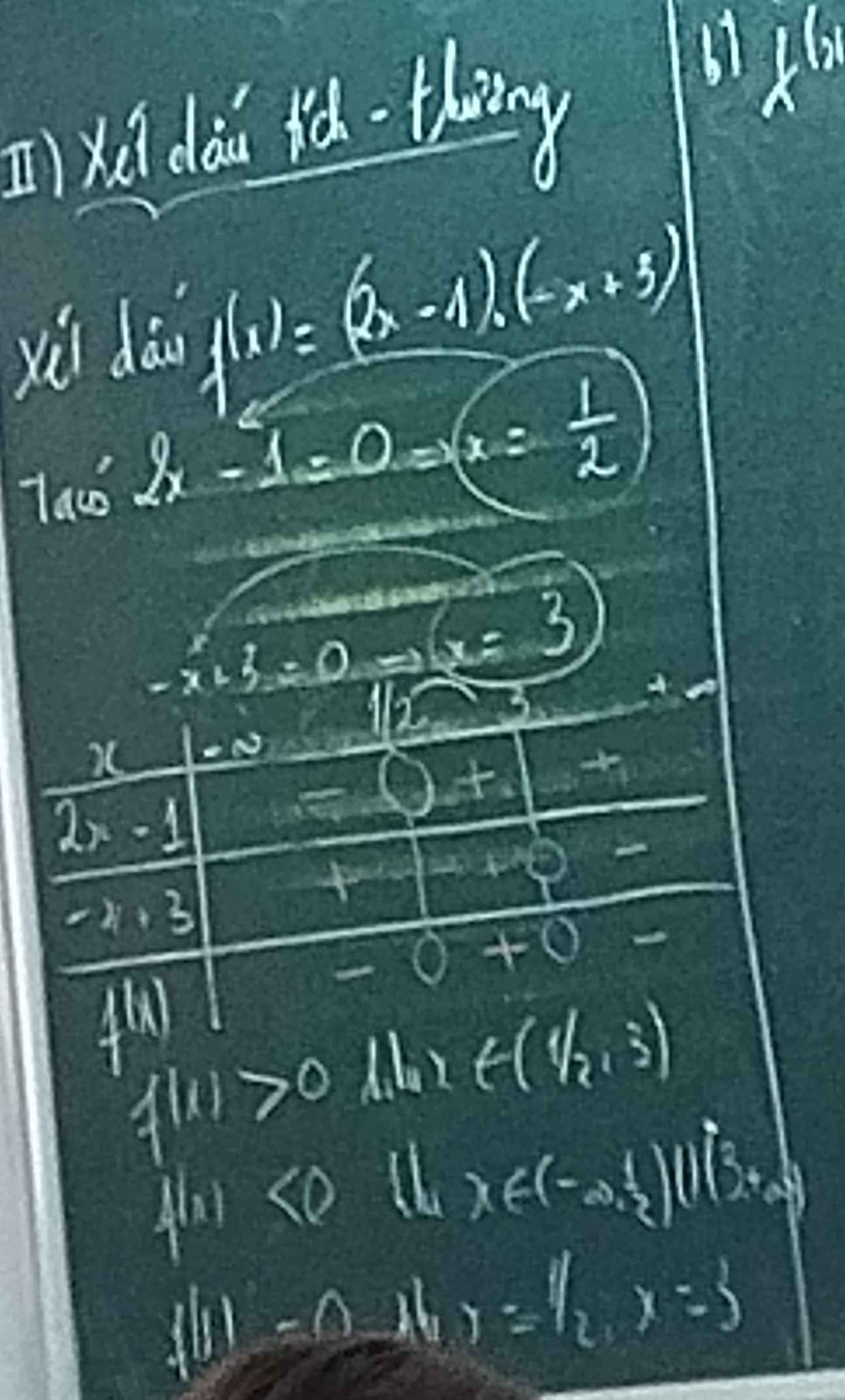
mọi ng giải giúp em câu e,f bài 1 với ạ
e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
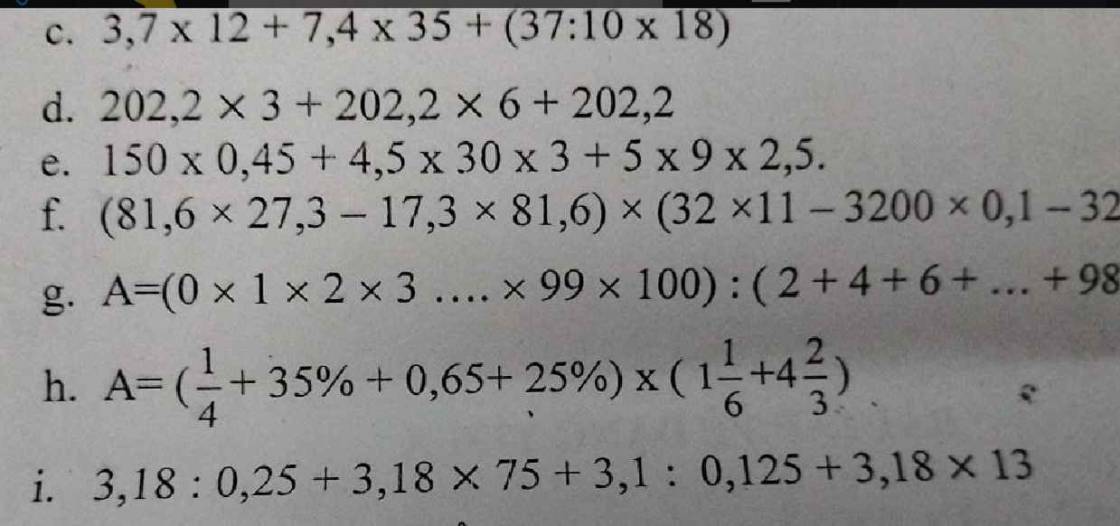 Giúp em với, bỏ câu (g) (h) cũng được ạ, giải mấy câu kia giúp em thuiii😢
Giúp em với, bỏ câu (g) (h) cũng được ạ, giải mấy câu kia giúp em thuiii😢
c: \(=3.7\cdot12+3.7\cdot70+3.7\cdot18\)
=3,7(12+70+18)
=3,7*100=370
d: \(=202,2\left(3+6+1\right)=202,2\cdot10=2022\)
e: \(=4,5\cdot15+4,5\cdot90+4,5\cdot25=4,5\left(15+90+25\right)=585\)
i: \(=3.18\cdot4+3.18\cdot75+3.1\cdot8+3.18\cdot13\)
\(=3,18\left(4+75+13\right)+24,8\)
\(=317.36\)

Chỉ giải hộ em câu : C , D , E , F , G , H ạ ;-; !
a: Ta có: \(\sqrt{75}-\sqrt{5\dfrac{1}{3}}+\dfrac{9}{2}\sqrt{2\dfrac{2}{3}}+2\sqrt{27}\)
\(=5\sqrt{3}+\dfrac{4}{3}\sqrt{3}+3\sqrt{6}+6\sqrt{3}\)
\(=\dfrac{37}{3}\sqrt{3}+3\sqrt{6}\)
c: Ta có: \(\left(\sqrt{12}+2\sqrt{27}\right)\cdot\dfrac{\sqrt{3}}{2}-\sqrt{150}\)
\(=\left(2\sqrt{3}+6\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2}-5\sqrt{6}\)
\(=12-5\sqrt{6}\)
Câu này lm kiểu gì ạ ! ai giải giúp em với ạ
Ai giúp em giải câu này với ạ???

Xét tính trạng hình dạng cây:
\(\dfrac{Cao}{Thap}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> Cao THT so với thấp
Quy ước gen: A cao. a thấp
Xét tính trạng màu sắc
\(\dfrac{Đỏ}{vang}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> đỏ THT so với vàng
Quy ước gen: B đỏ. b vàng
Vì F2 thu dc tỉ lệ 9:3:3:1
=> tuân theo quy luật phân li độc lập Của Menden
=> F1 dị hợp 2 cặp giao tử. kiểu gen F1: AaBb
F1 dị hợp 2 cặp giao tử => P thuần chủng
P Cao,đỏ. x. Thấp,vàng
AABB aabb
Gp AB ab
F1: AaBb( cao,đỏ)
F1 xF1 AaBb( cao,đỏ) x AaBb( cao,đỏ)
GF1 AB,Ab,aB ab AB,Ab,aB,ab
F2: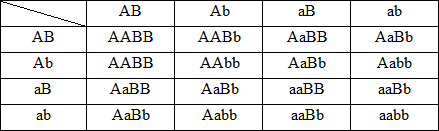
Kiểu gen: 9A_B_:3A_bb:3aaB_:1aabb
kiểu hình:9cao,đỏ :3 cao,vàng:3 thấp,đỏ:1 thấp,vàng
Ai giải giúp em câu 1234 với ạ
Câu 4.
Có \(N_1>N_2\Rightarrow\)Máy hạ thế.
Hiệu điện thế hai đầu cuộn sơ cấp:
\(\dfrac{U_1}{U_2}=\dfrac{N_1}{N_2}\Rightarrow\dfrac{1500}{250}=\dfrac{U_1}{220}\)
\(\Rightarrow U_1=1320V\)
Ai giúp em giải câu 32 với ạ :(
ABC vuông cân \(\Rightarrow\left\{{}\begin{matrix}AC=AB=3\\BC=AB\sqrt{2}=3\sqrt{2}\end{matrix}\right.\)
\(\overrightarrow{BC}.\overrightarrow{CA}=-\overrightarrow{CB}.\overrightarrow{CA}=-BC.AC.cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\sqrt{2}.3.cos45^0=-9\)